Cho tam giác ABC có \(\widehat B = 40^\circ ;\widehat C = 70^\circ \). Kẻ BD vuông góc với AC. Biết AD = 4 cm, tính độ dài cạnh AC.
-
A.
4 cm
-
B.
8 cm
-
C.
12 cm
-
D.
6 cm
Áp dụng định lí tổng ba góc trong tam giác, suy ra các góc bằng nhau.
Áp dụng trường hợp bằng nhau của tam giác vuông, suy ra các cạnh tương ứng bằng nhau
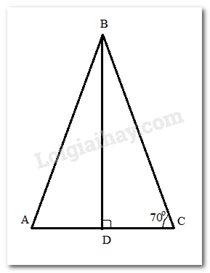
Xét tam giác ABC, có \(\widehat A + \widehat {ABC} + \widehat C = 180^\circ \) ( tổng 3 góc trong tam giác bằng 180 độ)
\(\begin{array}{l} \Rightarrow \widehat A + 40^\circ + 70^\circ = 180^\circ \\ \Rightarrow \widehat A = 70^\circ \\ \Rightarrow \widehat A = \widehat C\end{array}\)
Trong \(\Delta \)ABD vuông tại D, có \(\widehat A + \widehat {ABD} = 90^\circ \)
Trong \(\Delta \)CBD vuông tại D, có: \(\widehat C + \widehat {CBD} = 90^\circ \)
\( \Rightarrow \widehat {ABD} = \widehat {CBD}\)
Xét \(\Delta \)ABD và \(\Delta \)CBD , ta có:
\(\widehat {ADB} = \widehat {CDB}( = 90^\circ )\)
BD chung
\(\widehat {ABD} = \widehat {CBD}\)
\( \Rightarrow \)\(\Delta \)ABD = \(\Delta \)CBD ( g.c.g)
\( \Rightarrow \) AD = CD ( 2 cạnh tương ứng)
Mà AD = 4cm
\( \Rightarrow \)CD = 4 cm
Ta có:
AC = AD + CD = 4 + 4 = 8 ( cm)
Đáp án : B
