Cho góc nhọn \(xOy,Oz\) là tia phân giác của góc đó. Qua điểm \(A\) thuộc tia \(Ox\) kẻ đường thẳng song song với \(Oy\) cắt \(Oz\) ở \(M.\) Qua \(M\)kẻ đường thẳng song song với \(Ox\) cắt \(Oy\) ở \(B.\) Chọn câu đúng.
-
A.
\(OA > OB;MA > MB\)
-
B.
\(OA = OB;MA = MB\)
-
C.
\(OA < OB;MA < MB\)
-
D.
\(OA < OB;MA = MB\)
+ Từ tính chất đường thẳng song song, tính chất tia phân giác suy ra các cặp góc bằng nhau.
+ Dựa vào trường hợp bằng nhau thứ ba của tam giác và hệ quả của trường hợp bằng nhau thứ ba để chứng minh các tam giác bằng nhau để suy ra các cặp cạnh bằng nhau.
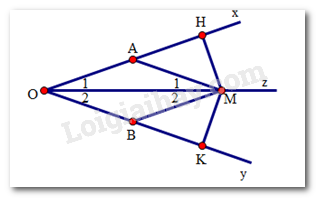
Ta có:
\(\widehat {{M_1}} = \widehat {{O_2}}\) (hai góc so le trong)
\(\widehat {{M_2}} = \widehat {{O_1}}\) (hai góc so le trong)
\(\widehat {{O_2}} = \widehat {{O_1}}\)(do Oz là tia phân giác của góc xOy)
Do đó \(\widehat {{M_2}} = \widehat {{M_1}}\)
Xét tam giác \(AOM\) và tam giác \(BOM\) có:
\(\widehat {{M_2}} = \widehat {{M_1}}\)(cmt)
\(OM\) là cạnh chung
\(\widehat {{O_2}} = \widehat {{O_1}}\)(cmt)
\( \Rightarrow \Delta AOM = \Delta BOM(g.c.g)\)
Do đó \(OA = OB;MA = MB\) (các cặp cạnh tương ứng).
Đáp án : B








Danh sách bình luận