Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} = \widehat {{B_1}}\) (tham khảo hình vẽ) là của định lý nào dưới đây?
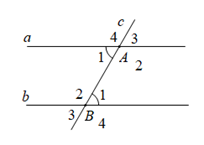
-
A.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song
-
B.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song.
-
C.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.
-
D.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Xét vị trí của góc A1 so với góc B1 rồi xét giả thiết của từng định lý
Đường thẳng c cắt đường thẳng a và b, tạo thành cặp góc so le trong bằng nhau (\(\widehat {{A_1}} = \widehat {{B_1}}\)) thì a // b
Vậy định lý là: “Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau thì hai đường thẳng đó song song”
Đáp án : B








Danh sách bình luận