Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
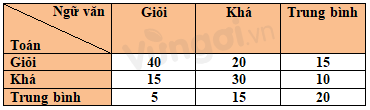
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:

Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Môn Toán đạt loại giỏi
-
A.
\(\dfrac{{15}}{{34}}\)
-
B.
\(\dfrac{4}{{17}}\)
-
C.
\(\dfrac{6}{{17}}\)
-
D.
\(\dfrac{{13}}{{34}}\)
Đáp án: A
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh được loại giỏi môn Toán.
- Xác suất thực nghiệm=Số học sinh được loại giỏi môn Toán:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Số học sinh được loại giỏi môn Toán là 40+20+15=75
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại giỏi môn Toán là \(\dfrac{{75}}{{170}} = \dfrac{{15}}{{34}}\)
Loại khá trở lên ở cả hai môn
-
A.
\(\dfrac{9}{{17}}\)
-
B.
\(\dfrac{7}{{17}}\)
-
C.
\(\dfrac{{21}}{{34}}\)
-
D.
\(\dfrac{7}{{34}}\)
Đáp án: C
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh loại khá trở lên ở cả 2 môn.
- Xác suất thực nghiệm=Số học sinh được loại khá trở lên ở cả 2 môn:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Các học sinh được loại khá trở lên ở cả 2 môn:
+ Toán giỏi, Ngữ văn giỏi: 40
+ Toán giỏi, Ngữ văn khá: 20
+ Toán khá, Ngữ văn giỏi: 15
+ Toán khá, Ngữ văn khá: 30
Số học sinh được loại khá trở lên ở cả 2 môn là:
40+20+15+30=105
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn là \(\dfrac{{105}}{{170}} = \dfrac{{21}}{{34}}\)
Loại trung bình ở ít nhất một môn
-
A.
\(\dfrac{{13}}{{17}}\)
-
B.
\(\dfrac{{13}}{{34}}\)
-
C.
\(\dfrac{{21}}{{34}}\)
-
D.
\(\dfrac{1}{2}\)
Đáp án: B
- Xét các trường hợp loại trung bình ở ít nhất một môn.
- Tính số học sinh được loại trung bình ở ít nhất một môn.
- Xác suất thực nghiệm=Số học sinh bị loại trung bình ở ít nhất 1 môn: Tổng số học sinh.
Tổng số học sinh là 170.
Các học sinh được loại trung bình ở ít nhất một môn là:
+ Toán trung bình, Văn giỏi: 5
+ Toán trung bình, Văn khá: 15
+ Toán trung bình, Văn trung bình: 20
+ Văn trung bình, Toán giỏi: 15
+ Văn trung bình, Toán khá: 10
Số học sinh được loại trung bình ở ít nhất một môn là:
5+15+20+15+10=65
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả được loại trung bình ít nhất một môn:
\(\dfrac{{65}}{{170}} = \dfrac{{13}}{{34}}\).

Các bài tập cùng chuyên đề
Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần |
8 |
7 |
3 |
12 |
10 |
10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
Gieo một con xúc xắc 20 lần liên tiếp, có 6 lần xuất hiện mặt 3 chấm thì xác suất thực nghiệm xuất hiện mặt 3 chấm bằng






