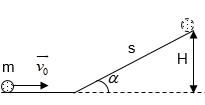
Một viên bi khối lượng m chuyển động trên mặt phẳng ngang không ma sát với vận tốc \(\overrightarrow {{v_0}} \) rồi đi lên mặt phẳng nhẵn và nghiêng góc \(\alpha \) (hình vẽ). Bi đi được quãng đường s thì dừng lại, khi đó nó có độ cao H so với mặt đất. Phương trình nào sau đây diễn tả định luật bảo toàn cơ năng của bi:
-
A.
\(\dfrac{1}{2}mv_0^2 = mgH\)
-
B.
\(\dfrac{1}{2}mv_0^2 - mgs = 0\)
-
C.
\(mgs.c{\rm{os}}\alpha = \dfrac{1}{2}mv_0^2\)
-
D.
\(\dfrac{1}{2}mv_0^2 = mgH.\sin \alpha \)
Cơ năng của vật chuyển động trong trọng trường :\(W = {W_d} + {W_t} = \dfrac{1}{2}m{v^2} + mgz\)
Khi một vật chuyển động trong trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật là một đại lượng bảo toàn.
Cơ năng của vật khi vật chuyển động trên mặt phẳng ngang: \(W = \dfrac{1}{2}mv_0^2\)
Cơ năng của vật khi vật ở độ cao h so với mặt đất: \(W' = mgH\)
Áp dụng định luật bảo toàn cơ năng ta có: \(W = W' \Leftrightarrow \dfrac{1}{2}mv_0^2 = mg.H\).
Đáp án : A
