1. Khái niệm tứ giác
Tứ giác là hình gồm bốn đoạn thẳng, trong đó không có hai đoạn thẳng nào cùng nằm trên một đường thẳng.
Ví dụ tứ giác:
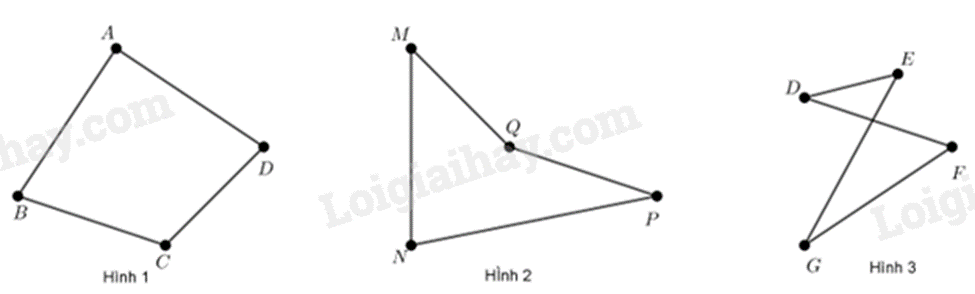
2. Khái niệm tứ giác lồi
Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của đường thẳng đi qua hai đỉnh còn lại.
Ví dụ:
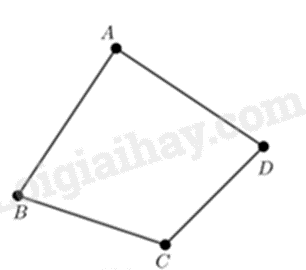
3. Khái niệm hình thang
Hình thang là tứ giác có hai cạnh đối song song.
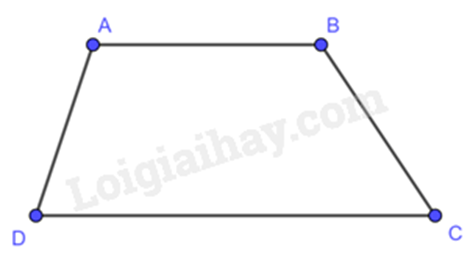
4. Khái niệm hình thang cân
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau; hai góc kề một cạnh bên thì bù nhau.
Ví dụ:
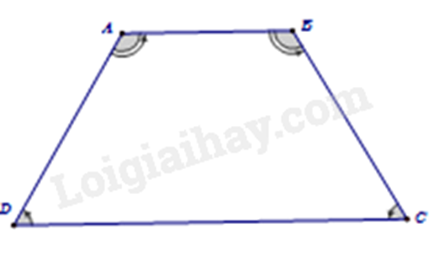
ABCD là hình thang cân thì \(\widehat A = \widehat B,\widehat C = \widehat D\).
5. Khái niệm hình bình hành
Hình bình hành là tứ giác có các cạnh đối song song.
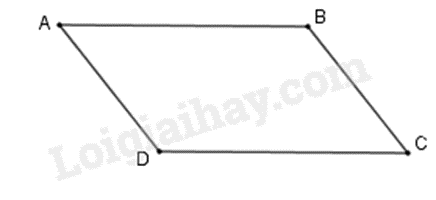
Ví dụ: Tứ giác ABCD là hình bình hành khi AB // CD và AD // BC.
6. Khái niệm hình chữ nhật
Hình chữ nhật là tứ giác có bốn góc vuông.
Lưu ý
Hình chữ nhật là một hình bình hành
Hình chữ nhật là một hình thang cân
Ví dụ:

Hình chữ nhật ABCD có:
+ bốn góc vuông: \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \).
+ hai cạnh đối song song: AB // CD và AD // BC.
+ hai cạnh đối bằng nhau: AB = CD và AD = BC.
+ hai đường chéo là AC, BD.
7. Khái niệm hình thoi
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Hình thoi cũng là một hình bình hành.
Ví dụ:
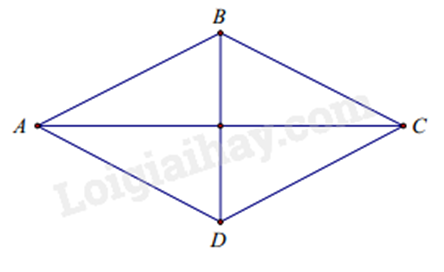
Xét hình thoi ABCD có:
+ Bốn cạnh bằng nhau: AB = BC = CD = DA .
+ Hai góc đối nhau: \(\widehat A\) và \(\widehat C\); \(\widehat B\) và \(\widehat D\).
+ Hai đường chéo: AC và BD .
+ Hai cạnh đối nhau: AB và CD ; BC và AD .
8. Khái niệm hình vuông
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
+ Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
+ Hình vuông là hình thoi có một góc vuông.
Như vậy, hình vuông vừa là hình chữ nhật, vừa là hình thoi.
Ví dụ:
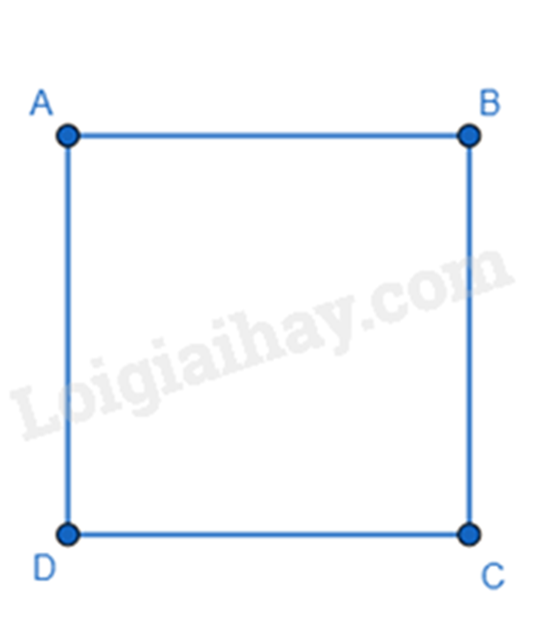
Cho ABCD là hình vuông, khi đó:
+ Bốn cạnh bằng nhau: AB = BC = CD = DA
+ Bốn góc bằng nhau và bằng \(90^\circ \): \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \).
9. Sơ đồ nhận biết các loại tứ giác


 Hình vuông - Từ điển môn Toán 8
Hình vuông - Từ điển môn Toán 8 





