Giải mục 4 trang 56 SGK Toán 10 tập 2 - Kết nối tri thức

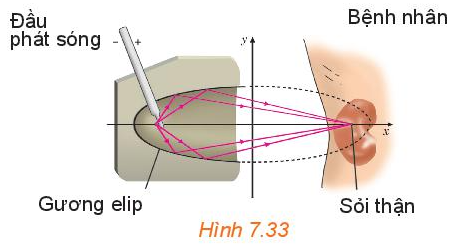
Gương elip trong một máy tán sỏi thận (H7.33) ứng với clip có phương trình chính tắc

Đề bài

Vận dụng 3 trang 56 SGK Toán 10 - Kết nối tri thức

Gương elip trong một máy tán sỏi thận (H7.33) ứng với clip có phương trình chính tắc là \(\frac{{{x^2}}}{{400}} + \frac{{{y^2}}}{{76}} = 1\) (theo đơn vị cm). Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.

Phương pháp giải - Xem chi tiết

Vị tri bắt đầu phát sóng của máy và vị trí viên sỏi được đặt ở hai tiêu điểm của gương elip, do đó khoảng cách cần tìm là tiêu cự của gương và bằng 2c.

\({a^2} = 400\), \({b^2} = 76\)

Từ phương trình chính tắc của elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), xác định \({a^2}\), \({b^2}\) rồi áp dụng công thức \(c = \sqrt {{a^2} - {b^2}} \).

Lời giải chi tiết

Từ phương trình chính tắc \(\frac{{{x^2}}}{{400}} + \frac{{{y^2}}}{{76}} = 1\), ta suy ra \({a^2} = 400\), \({b^2} = 76\).

Vị tri bắt đầu phát sóng của máy và vị trí viên sỏi được đặt ở hai tiêu điểm của gương elip, do đó khoảng cách cần tìm là tiêu cự của gương và bằng \(2c = 2\sqrt {400 - 76} = 36\) (cm).

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 6 phiếu

Bài tiếp theo

Giải bài 7.19 trang 56 SGK Toán 10 – Kết nối tri thức
Tìm tiêu điểm và tiêu cự của elip.
Giải bài 7.20 trang 56 SGK Toán 10 – Kết nối tri thức
Tìm tiêu điểm và tiêu cự của hyperbol.
Giải bài 7.21 trang 56 SGK Toán 10 – Kết nối tri thức
Tìm tiêu điểm và đường chuẩn của parabol
Giải bài 7.22 trang 56 SGK Toán 10 – Kết nối tri thức
Lập phương trình chính tắc của elip đi qua hai điểm
Giải bài 7.23 trang 56 SGK Toán 10 – Kết nối tri thức
Lập phương trình chính tắc của parabol đi qua điểm M(2;4)
Giải bài 7.24 trang 56 SGK Toán 10 – Kết nối tri thức
Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km.
Giải bài 7.25 trang 56 SGK Toán 10 – Kết nối tri thức
Khúc của của một con đường có dạng hình parabol, điềm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400 m. Đỉnh parabol (P) của khúc của cách đường thẳng ABmột khoảng 20 m và cách đều A, B (H.7.34).
Giải mục 3 trang 52, 53 SGK Toán 10 tập 2 - Kết nối tri thức
Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gi? Vì sao?
Giải mục 2 trang 50, 51, 52 SGK Toán 10 tập 2 - Kết nối tri thức
Tại sao trong định nghĩa hypebol cần điều kiện a
Giải mục 1 trang 48, 49, 50 SGK Toán 10 tập 2 - Kết nối tri thức
Kéo căng sợi dây tại một điểm M bởi một đầu bút dạ (hoặc phấn). Di chuyên đầu bút dạ để nó vẽ trên mặt bàn một đường khép kín (H7.18).
Lý thuyết Ba đường conic - SGK Toán 10 Kết nối tri thức
1. Elip a) Định nghĩa elip