 Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
 Bài 2. Tứ giác nội tiếp - Toán 9 Chân trời sáng tạo
Bài 2. Tứ giác nội tiếp - Toán 9 Chân trời sáng tạo
Giải bài tập 2 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác nhọn ABC. Gọi A’, B’, C’ lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp trong hình.
Tổng hợp Đề thi vào 10 có đáp án và lời giải
Toán - Văn - Anh
Đề bài
Cho tam giác nhọn ABC. Gọi A’, B’, C’ lần lượt là chân đường cao kẻ từ A, B, C và H là trực tâm của tam giác đó. Hãy chỉ ra các tứ giác nội tiếp trong hình.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào: Dựa vào một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp.
Lời giải chi tiết
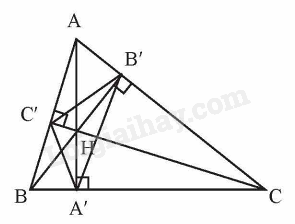
Ta có \( \Delta AB'H \) vuông tại \( B' \) và \( \Delta AC'H \) vuông tại \( C' \) cùng nội tiếp đường tròn đường kính \( AH \), suy ra tứ giác \( AB'HC' \) nội tiếp đường tròn đường kính \( AH \).
Tương tự, ta có tứ giác \( BA'HC' \) nội tiếp đường tròn đường kính \( BH \) và tứ giác \( CA'HB' \) nội tiếp đường tròn đường kính \( CH \).
Ta lại có \( \Delta AB'B \) vuông tại \( B' \) và \( \Delta AA'B \) vuông tại \( A' \) cùng nội tiếp đường tròn đường kính \( AB \), suy ra tứ giác \( AB'A'B \) nội tiếp đường tròn đường kính \( AB \).
Tương tự, ta có tứ giác \( BC'B'C \) nội tiếp đường tròn đường kính \( BC \) và tứ giác \( AC'A'C \) nội tiếp đường tròn đường kính \( AC \).
- Giải bài tập 3 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải bài tập 4 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải bài tập 5 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải bài tập 6 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải bài tập 7 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay











