SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống Bài 26. Khoảng cách - SBT Toán 11 KNTT

Giải bài 7.31 trang 38 sách bài tập toán 11 - Kết nối tri thức với cuộc sống


Cho hình lăng trụ đứng \(ABC \cdot A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\) và \(AB = AC = AA' = a\).

Đã có lời giải SGK Toán lớp 12 - Kết nối tri thức (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Cho hình lăng trụ đứng \(ABC \cdot A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\) và \(AB = AC = AA' = a\). Tính theo a khoảng cách:

a) Từ điểm \(A\) đến đường thẳng \(B'C'\).

b) Giữa hai đường thẳng \(BC\) và \(AB'\).

Phương pháp giải - Xem chi tiết

a)     Tính khoảng cách từ điểm \(A\) đến đường thẳng \(B'C'\).

Bước 1: Tìm hình chiếu của điểm trên đường thẳng \(B'C'\).

Kẻ \(AH\) vuông góc với \(B'C'\) tại \(H\) thì \(d\left( {A,B'C'} \right) = AH\).

Bước 2: Tính \(AH\)

b) Tính khoảng cách giữa hai đường thẳng \(BC\) và \(AB'\).

Bước 1:  Dựng mặt phẳng qua đường thẳng \(AB'\) và song song với  \(BC\) là \(\left( {AB'C'} \right)\)

Chuyển khoảng cách về chân đường vuông góc

\(d\left( {BC,AB'} \right) = d\left( {BC,\left( {AB'C'} \right)} \right) = d\left( {C,\left( {AB'C'} \right)} \right) = d\left( {C,\left( {AB'C'} \right)} \right) = d\left( {A',\left( {AB'C'} \right)} \right).\)

Bước 2: Tính \(d\left( {A',\left( {AB'C'} \right)} \right)\)

Lời giải chi tiết

a) Kẻ \(AH\) vuông góc với \(B'C'\) tại \(H\) thì \(d\left( {A,B'C'} \right) = AH\).

Ta có: \(AB' = AC' = B'C' = a\sqrt 2 \) nên \(AH = \frac{{a\sqrt 6 }}{2}\).

Vậy \(d\left( {A,B'C'} \right) = \frac{{a\sqrt 6 }}{2}\).

b) Vì \(BC//\left( {AB'C'} \right)\) nên \(d\left( {BC,AB'} \right) = d\left( {BC,\left( {AB'C'} \right)} \right) = d\left( {C,\left( {AB'C'} \right)} \right).\)

 

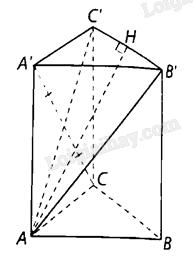
Mà \(CA'\) cắt \(AC'\) tại trung điểm của \(CA'\) nên \(d\left( {C,\left( {AB'C'} \right)} \right) = d\left( {A',\left( {AB'C'} \right)} \right)\)

Đặt \(d\left( {A',\left( {AB'C'} \right)} \right) = h\) thì \(\frac{1}{{{h^2}}} = \frac{1}{{A'{A^2}}} + \frac{1}{{A'{B^{{\rm{'}}2}}}} + \frac{1}{{A'{C^{{\rm{'}}2}}}} = \frac{3}{{{a^2}}}\), suy ra \(h = \frac{{a\sqrt 3 }}{3}\).

Vậy \(d\left( {BC,AB'} \right) = \frac{{a\sqrt 3 }}{3}\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua