-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống
Bài tập ôn tập cuối năm - SBT Toán 11 KNTT
Giải bài 39 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), đường thẳng \(SA\). vuông góc vói mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).
Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), đường thẳng \(SA\). vuông góc vói mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).
a) Chứng minh rằng \(\left( {SBC} \right) \bot \left( {SAB} \right)\).
b) Tính góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\).
Tính theo \(a\) khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
Phương pháp giải - Xem chi tiết
a) Chứng minh \(BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\).
b) Tìm hình chiếu vuông góc của \(SC\) trên mặt phẳng \(\left( {ABCD} \right)\) là \(AC\),
Suy ra góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) là góc giữa hai đường thẳng \(SC\) và \(AC\).
Chứng minh tam giác \(SAC\) vuông cân tại \(A\), suy ra \(\widehat {SCA}\)
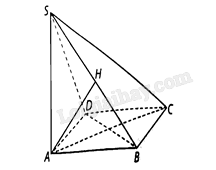
c) Kẻ \(AH\) vuông góc với \(SB\) tại \(H\), chứng minh \(AH \bot \left( {SBC} \right)\).
Suy ra khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(AH\).
Xét tam giác \(SAB\) vuông tại \(A\), tính đường cao \(AH\)
Lời giải chi tiết
a) Vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC\) mà \(BC \bot AB \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\).
b) Vì \(SA \bot \left( {ABCD} \right)\) nên đường thẳng \(AC\) là hình chiếu vuông góc của \(SC\) trên mặt phẳng \(\left( {ABCD} \right)\), do đó góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) là góc giứa hai đường thẳng \(SC\) và \(AC\).
Ta có: \(SA \bot AC\) và \(SA = AC = a\sqrt 2 \) nên tam giác \(SAC\) vuông cân tại \(A\), suy ra góc giữa hai đường thẳng \(SC\) và \(AC\) bằng \({45^ \circ }\).
Vậy góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^ \circ }\).
c) Kẻ \(AH\) vuông góc với \(SB\) tại \(H\), vì \(BC \bot \left( {SAB} \right)\) nên \(BC \bot AH\), suy ra \(AH \bot \left( {SBC} \right)\).
Do đó khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng \(AH\).
Xét tam giác \(SAB\) vuông tại \(A\), có đường cao \(AH\), khi đó:
\(AH = \frac{{SA \cdot AB}}{{SB}} = \frac{{a \cdot a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{3}.\)
Bình luận
Chia sẻ
- Giải bài 40 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 41 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 42 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 43 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 38 trang 71 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải bài 43 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 39 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 40 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 41 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 42 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 43 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 42 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 41 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 40 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
- Giải bài 39 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
