SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống Bài tập ôn tập cuối năm - SBT Toán 11 KNTT

Giải bài 21 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống


Cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), cạnh bên \(SA\) bằng \(a\sqrt 2 \). Khoảng cách giữa hai đường thẳng \(BD\) và \(SC\) là

Đề bài

Cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), cạnh bên \(SA\) bằng \(a\sqrt 2 \). Khoảng cách giữa hai đường thẳng \(BD\) và \(SC\) là

A. \(\frac{{a\sqrt 6 }}{4}\).

B. \(\frac{{a\sqrt 6 }}{3}\).

C. \(\frac{{a\sqrt 6 }}{2}\).

D. \(\frac{{a\sqrt 3 }}{2}\).

Phương pháp giải - Xem chi tiết

Chứng minh \(BD \bot \left( {SAC} \right)\) tại \(O\). Kẻ \(OH \bot SC,H \in SC\).

Chứng minh \(OH\) là đoạn vuông góc chung của \(BD\) và \(SC\)

Tính \(OH\)

Lời giải chi tiết

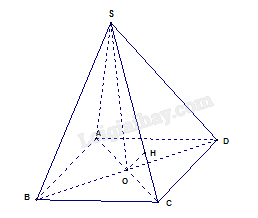
Ta có \(\left\{ \begin{array}{l}SO \bot \left( {ABCD} \right)\\BD \bot AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}SO \bot BD\\BD \bot AC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\)

Kẻ \(OH \bot SC,H \in SC\)

Ta có \(\left\{ \begin{array}{l}BD \bot \left( {SAC} \right)\\OH \subset \left( {SAC} \right)\end{array} \right. \Rightarrow OH \bot BD\)

Khoảng cách giữa hai đường thẳng \(BD\) và \(SC\) là \(OH\)

Có \(SO \bot AC \Rightarrow SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {2{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}  = \frac{{a\sqrt 6 }}{2}\)

\(OH = \frac{{SO.OC}}{{\sqrt {S{O^2} + O{C^2}} }} = \frac{{\frac{{a\sqrt 6 }}{2}.\frac{{a\sqrt 2 }}{2}}}{{\sqrt {{{\left( {\frac{{a\sqrt 6 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} }} = \frac{{a\sqrt 6 }}{4}\)

Chọn A


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store