 SBT Toán 9 - giải SBT Toán 9 - Kết nối tri thức với cuộc sống
SBT Toán 9 - giải SBT Toán 9 - Kết nối tri thức với cuộc sống
 Bài 16. Vị trí tương đối của đường thẳng và đường tròn ..
Bài 16. Vị trí tương đối của đường thẳng và đường tròn ..
Giải bài 5.21 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC vuông tại A, có đường cao AH. a) Chứng minh rằng BC tiếp xúc với đường tròn (A) bán kính AH; b) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Chứng minh rằng BM và CN là hai tiếp tuyến của (A); c) Chứng minh rằng MN là một đường kính của (A); d) Tính diện tích của tứ giác BMNC, biết (HB = 2cm) và (HC = 4,5cm).
Đề bài
Cho tam giác ABC vuông tại A, có đường cao AH.
a) Chứng minh rằng BC tiếp xúc với đường tròn (A) bán kính AH;
b) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Chứng minh rằng BM và CN là hai tiếp tuyến của (A);
c) Chứng minh rằng MN là một đường kính của (A);
d) Tính diện tích của tứ giác BMNC, biết \(HB = 2cm\) và \(HC = 4,5cm\).
Phương pháp giải - Xem chi tiết
a) + Chỉ ra \(AH \bot BC\) tại H, H thuộc (A, AH) nên BC tiếp xúc với đường tròn (A) bán kính AH.
b) + Chứng minh \(\Delta AMB = \Delta AHB\left( {c.c.c} \right)\).
Do đó, \(\widehat {AMB} = \widehat {AHB} = {90^o}\).
+ Chứng minh M thuộc đường tròn (A). Suy ra, BM vuông góc với AM tại M nên BM là tiếp tuyến của (A) tại M.
+ Chứng minh \(\Delta ANC = \Delta AHC\left( {c.c.c} \right)\).
Do đó, \(\widehat {ANC} = \widehat {AHC} = {90^o}\).
+ Chỉ ra N thuộc đường tròn (A).
+ Suy ra, CN vuông góc với AN tại N nên AN là tiếp tuyến của (A) tại N.
c) + Chứng minh \(\widehat {MAB} = \widehat {HAB}\), \(\widehat {NAC} = \widehat {HAC}\), \(\widehat {HAB} + \widehat {HAC} = {90^o}\).
+ Do đó, \(\widehat {MAB} + \widehat {HAB} + \widehat {NAC} + \widehat {HAC} = {180^o}\)
+ Suy ra, ba điểm M, A, N thẳng hàng. Vậy MN là đường kính của (A).
d) + Chứng minh \(BM = BH\), \(CN = CH\).
+ Do đó, \(BM + CN = BH + CH = 2 + 4,5 = 6,5\left( {cm} \right)\)
+ Chứng minh $\Delta HBA\backsim \Delta HAC\left( g.g \right)$ nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\), từ đó tính được AH, tính được MN.
+ Chứng minh tứ giác BMNC là hình thang vuông.
+ Diện tích hình thang BMNC là: \(S = \frac{1}{2}MN\left( {BM + CN} \right)\).
Lời giải chi tiết
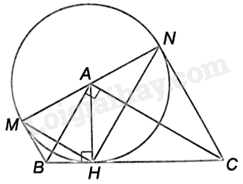
a) Vì AH là đường cao của tam giác ABC nên \(AH \bot BC\) tại H. Mà H thuộc (A, AH) nên BC tiếp xúc với đường tròn (A) bán kính AH.
b) Vì M đối xứng với H qua AB nên \(AM = AH\) và \(BM = BH\), AB chung nên \(\Delta AMB = \Delta AHB\left( {c.c.c} \right)\).
Do đó, \(\widehat {AMB} = \widehat {AHB} = {90^o}\).
Lại có \(AM = AH\) nên M thuộc đường tròn (A).
Suy ra, BM vuông góc với AM tại M nên BM là tiếp tuyến của (A) tại M.
Vì N đối xứng với H qua AC nên \(CN = CH\) và \(AH = AN\), AC chung nên \(\Delta ANC = \Delta AHC\left( {c.c.c} \right)\).
Do đó, \(\widehat {ANC} = \widehat {AHC} = {90^o}\).
Lại có \(AH = AN\) nên N thuộc đường tròn (A).
Suy ra, CN vuông góc với AN tại N nên AN là tiếp tuyến của (A) tại N.
c) Vì \(\Delta AMB = \Delta AHB\left( {cmt} \right)\) nên \(\widehat {MAB} = \widehat {HAB}\).
Vì \(\Delta ANC = \Delta AHC\left( {cmt} \right)\) nên \(\widehat {NAC} = \widehat {HAC}\).
Vì \(AH \bot BC\) tại H nên \(\widehat {HAB} + \widehat {HAC} = {90^o}\).
Do đó, \(\widehat {MAB} + \widehat {HAB} + \widehat {NAC} + \widehat {HAC} \) \(= 2\left( {\widehat {HAB} + \widehat {HAC}} \right) \) \(= {2.90^o} = {180^o}\)
Suy ra, ba điểm M, A, N thẳng hàng.
Mà \(AM = AN\left( { = AH} \right)\) nên MN là đường kính của (A).
d) Vì MB và BH là hai tiếp tuyến cắt nhau tại B của (A) nên \(BM = BH\).
Vì CN và CH là hai tiếp tuyến cắt nhau tại C của (A) nên \(CN = CH\).
Do đó, \(BM + CN = BH + CH = 2 + 4,5 = 6,5\left( {cm} \right)\).
Ta có:
\(\widehat {BAH} + \widehat {ABC} = \widehat {ACH} + \widehat {ABC}\\\left( { = {{90}^o}} \right)\) nên \(\widehat {BAH} = \widehat {ACH}\).
Mà \(\widehat {BHA} = \widehat {CHA} = {90^o}\) nên $\Delta HBA\backsim \Delta HAC\left( g.g \right)$
nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\),
suy ra \(A{H^2} = BH.CH = 4,5.2 = 9\).
Suy ra \(AH = 3cm\).
Do đó, \(MN = 2AH = 6cm\).
Ta có: \(BM \bot MN,CN \bot MN\) nên BM//NC.
Do đó, tứ giác BMNC là hình thang vuông.
Diện tích hình thang BMNC là:
\(S = \frac{1}{2}MN\left( {BM + CN} \right) = \frac{1}{2}.6.6,5 = 19,5\left( {c{m^2}} \right)\).
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 18 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 17 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 16 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 15 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 14 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 18 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 17 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 16 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 15 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 14 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2











