Giải bài 5.20 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1

Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết (AB = 10cm), (AC = 7cm) và (BC = 6cm). Tính độ dài của các đoạn thẳng AM, AN, BM và CN.

Đề bài

Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết \(AB = 10cm\), \(AC = 7cm\) và \(BC = 6cm\). Tính độ dài của các đoạn thẳng AM, AN, BM và CN.

Phương pháp giải - Xem chi tiết

+ Dựa vào tính chất hai tiếp tuyến cắt nhau ta có \(AM = AN\), \(BM = BE\), \(CE = CN\).

+ \(AM + AN = AB + AC + CE\), từ đó tính được AM, AN.

+ \(BM = AM - AN,CN = AN - CN\).

Lời giải chi tiết

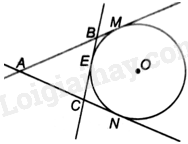
Vì AM và AN là hai tiếp tuyến cắt nhau của (O) nên \(AM = AN\).

Vì BM và BE là hai tiếp tuyến cắt nhau của (O) nên \(BM = BE\).

Vì CE và CN là hai tiếp tuyến cắt nhau của (O) nên \(CE = CN\).

Ta có:

\(AM + AN = AB + BM + AC + CN \)

\(= AB + BE + AC + CE = AB + AC + \left( {BE + CE} \right)\)

\( = AB + AC + BC\)

Suy ra \(2AM = 10 + 7 + 6 = 23\left( {cm} \right)\) nên \(AM = AN = 11,5\left( {cm} \right)\)

\(BM = AM - AB = 11,5 - 10 = 1,5\left( {cm} \right),\)

\(CN = AN - AC = 11,5 - 7 = 4,5\left( {cm} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4 trên 4 phiếu

Bài tiếp theo

Giải bài 5.21 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC vuông tại A, có đường cao AH. a) Chứng minh rằng BC tiếp xúc với đường tròn (A) bán kính AH; b) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Chứng minh rằng BM và CN là hai tiếp tuyến của (A); c) Chứng minh rằng MN là một đường kính của (A); d) Tính diện tích của tứ giác BMNC, biết (HB = 2cm) và (HC = 4,5cm).
Giải bài 5.19 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn (O) và điểm M nằm bên ngoài (O). Từ M kẻ tiếp tuyến MA với (O), trong đó A là tiếp điểm. Đường thẳng qua A và vuông góc với MO cắt (O) tại B (khác A). a) Chứng minh rằng MB là tiếp tuyến của (O); b) Tính OM và diện tích phần của tam giác AMB nằm bên ngoài (O), biết bán kính của (O) bằng 3cm và (widehat {MAB} = {60^o}).
Giải bài 5.18 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường thẳng a, điểm M thuộc a và số dương R. Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho (AM = R) (đvđd). Chứng minh rằng đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?
Giải bài 5.17 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn (O) và điểm P. a) Giả sử (P in left( O right)). Vẽ đường thẳng a đi qua P và vuông góc với OP. Chứng minh rằng a là tiếp tuyến của đường tròn (O) tại P. b) Giả sử P nằm ngoài (O). Vẽ đường tròn đường kính OP. Đường tròn vừa vẽ cắt (O) tại A và B. Chứng minh rằng PA và PB là hai tiếp tuyến của (O).