Giải bài 4.15 trang 59 SGK Toán 10 tập 1 – Kết nối tri thức

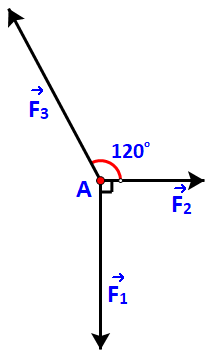
Chất điểm A chịu tác động của ba lực F1, F2, F3 như hình 4.30 và ở trạng thái cân bằng

Đề bài

Chất điểm A chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) như hình 4.30 và ở trạng thái cân bằng (tức là \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)). Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) biết \(\overrightarrow {{F_1}} \) có độ lớn là 20N.

Phương pháp giải - Xem chi tiết

Bước 1: Xác định vecto \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Từ trạng thái của chất điểm suy ra mối liên hệ (phương, chiều, độ lớn) giữa \(\overrightarrow u \) và \(\overrightarrow {{F_3}} \).

Bước 2: Tính độ lớn của \(\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \).

Lời giải chi tiết

Bước 1: Đặt \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Ta xác định các điểm như hình dưới.

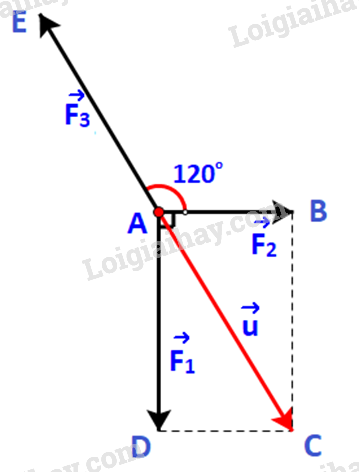
Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto \(\overrightarrow u \) chính là vecto \(\overrightarrow {AC} \)

Vì chất điểm A ở trang thái cân bằng nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\;\overrightarrow u + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)

\( \Leftrightarrow \;\overrightarrow u \) và \(\;\overrightarrow {{F_3}} \) là hai vecto đối nhau.

\( \Leftrightarrow A\) là trung điểm của EC.

Bước 2:

Ta có: \(\left| {\overrightarrow {{F_1}} } \right| = AD = 20,\;\left| {\overrightarrow {{F_2}} } \right| = AB,\;\left| {\overrightarrow {{F_3}} } \right| = AC.\)

Do A, C, E thẳng hàng nên \(\widehat {CAB} = {180^o} - \widehat {EAB} = {60^o}\)

\(\begin{array}{l} \Rightarrow \widehat {CAD} = {90^o} - {60^o} = {30^o}\\ \Rightarrow \left\{ \begin{array}{l}AC = \frac{{AD}}{{\cos {{30}^o}}} = \frac{{40\sqrt 3 }}{3};\;\\AB = DC = AC.\sin {30^o} = \frac{{20\sqrt 3 }}{3}.\end{array} \right.\end{array}\)

Vậy \(\;\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3},\;\;\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}.\)

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 13 phiếu

Bài tiếp theo

Giải bài 4.14 trang 58 SGK Toán 10 tập 1 – Kết nối tri thức
Cho tam giác ABC a) Hãy xác định điểm M để MA +MB+2MC=0 b) Chứng minh rằng với mọi điểm O, ta có OA+OB+2OC = 4OM
Giải bài 4.13 trang 58 SGK Toán 10 tập 1 – Kết nối tri thức
Cho hai điểm phân biệt A và B.
Giải bài 4.12 trang 58 SGK Toán 10 tập 1 – Kết nối tri thức
Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh
Giải bài 4.11 trang 58 SGK Toán 10 tập 1 – Kết nối tri thức
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị AM theo hai vecto AB và AD.
Giải mục 2 trang 57, 58, 59 SGK Toán 10 tập 1 - Kết nối tri thức
Với u khác 0 và hai số thực k, t, những khẳng định nào sau đây là đúng? Hãy chỉ ra trên Hình 4.26 hai vecto 3u+v và 3u + 3v. Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có Trong hình 4.27, hãy biểu thị mỗi vecto u ,v theo hai vecto a, b
Giải mục 1 trang 55, 56 SGK Toán 10 tập 1 - Kết nối tri thức
1a và a có bằng nhau hay không? Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số 0, 1, . Hãy nêu mối quan hệ về hướng và độ dài -a và -1a có mối quan hệ gì? Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
Lý thuyết Tích của vecto mới một số - SGK Toán 10 Kết nối tri thức
1. TÍCH CỦA VECTO VỚI MỘT SỐ 2. CÁC TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ