Giải bài 3 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo
Lập bảng biến thiên của hàm số y = x^2 + 2x + 3. Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Phương pháp giải - Xem chi tiết
Với \(a = 1 > 0\), hàm số có bảng biến thiên dạng:
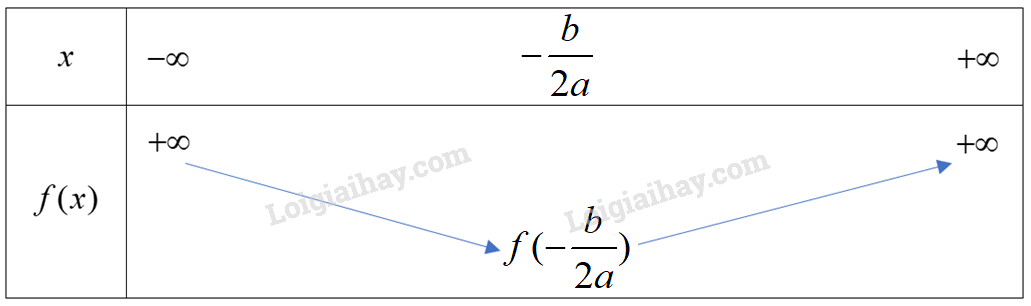
Hàm số đạt giá trị nhỏ nhất bằng \(f( - \frac{b}{{2a}})\) tại \(x = - \frac{b}{{2a}}.\)
Lời giải chi tiết
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
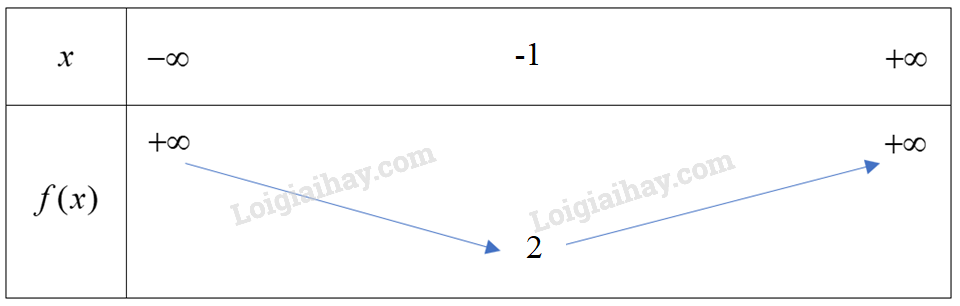
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
- Giải bài 4 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo
- Giải bài 5 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo
- Giải bài 6 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo
- Giải bài 7 trang 56 SGK Toán 10 tập 1 – Chân trời sáng tạo
- Giải bài 8 trang 57 SGK Toán 10 tập 1 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo












