Giải bài 3 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo

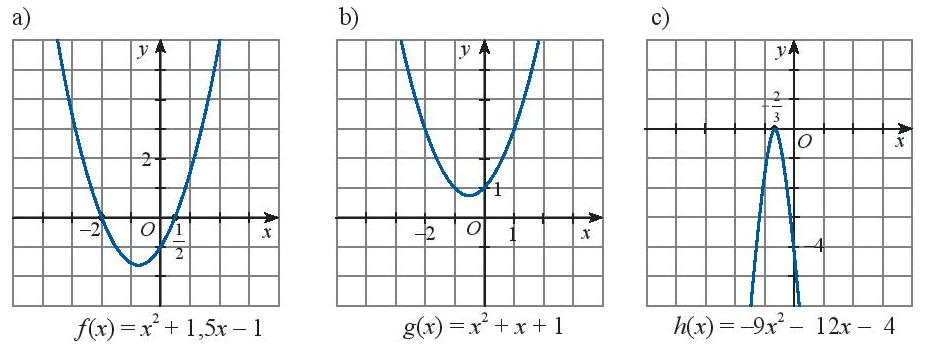
Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng

Đề bài

Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng

Phương pháp giải - Xem chi tiết

Bước 1: Xác định nghiệm của tam thức (là giao điểm của đồ thị với trục hoành)

Bước 2: Xác định khoảng mà \(f\left( x \right) > 0\) (khoảng đồ thị nằm trên trục hoành)

Bước 3: Xác định khoảng mà \(f\left( x \right) < 0\) (khoảng đồ thị nằm dưới trục hoành)

Bước 4: Lập bảng xét dấu

Lời giải chi tiết

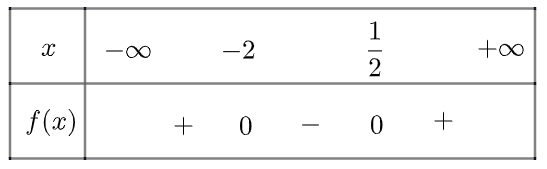
a) Tam thức \(f\left( x \right) = {x^2} + 1,5x - 1\) có hai nghiệm phân biệt \({x_1} = - 2;{x_2} = \frac{1}{2}\)

\(\)\(f\left( x \right) > 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{1}{2}, + \infty } \right)\) và \(f\left( x \right) < 0\) khi \(x \in \left( { - 2,\frac{1}{2}} \right)\)

Ta có bảng xét dấu như sau

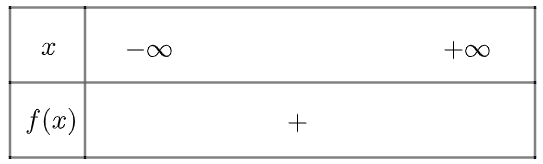
b) Tam thức \(g\left( x \right) = {x^2} + x + 1\) vô nghiệm, \(g\left( x \right) > 0\forall x \in \mathbb{R}\)

Ta có bảng xét dấu như sau

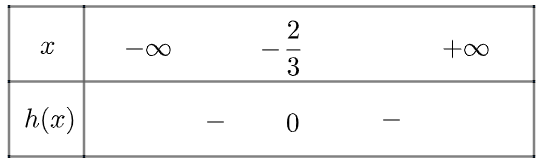
c) Tam thức \(h\left( x \right) = - 9{x^2} - 12x - 4\) có nghiệm kép \({x_1} = {x_2} = - \frac{2}{3}\) và \(h\left( x \right) < 0\forall x \ne - \frac{2}{3}\)

Ta có bảng xét dấu như sau

d) Tam thức \(f\left( x \right) = - 0,5{x^2} + 3x - 6\) vô nghiệm và \(f\left( x \right) < 0\forall x \in \mathbb{R}\)

Ta có bảng xét dấu như sau:

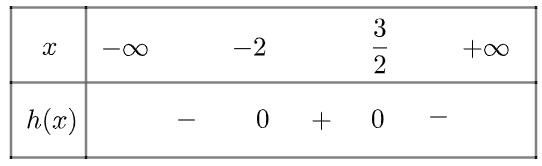
e) Tam thức \(g\left( x \right) = - {x^2} - 0,5x + 3\) có hai nghiệm \({x_1} = - 2,{x_2} = \frac{3}{2}\)

\(g\left( x \right) > 0\) khi \(x \in \left( { - 2,\frac{3}{2}} \right)\) và \(g\left( x \right) < 0\) khi \(x \in \left( { - \infty , - 2} \right) \cup \left( {\frac{3}{2}, + \infty } \right)\)

Ta có bảng xét dấu như

g) Tam thức \(h\left( x \right) = {x^2} + 2\sqrt 2 x + 2\) có nghiệm kép \({x_1} = {x_2} = - \sqrt 2 \)

\(h\left( x \right) > 0\forall x \ne - \sqrt 2 \)

Ta có bảng xét dấu như sau

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 9 phiếu

Bài tiếp theo

Giải bài 4 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo
Xét dấu của các tam thức bậc hai sau đây:
Giải bài 5 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo
Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng bằng hàm số
Giải bài 6 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo
Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm được uốn lại thành hình chữ nhật mới có kích thước
Giải bài 7 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo
Chứng minh rằng với mọi số thực m ta luôn có
Giải bài 8 trang 10 SGK Toán 10 tập 2 – Chân trời sáng tạo
Tìm giá trị của m để
Giải bài 2 trang 9 SGK Toán 10 tập 2 – Chân trời sáng tạo
Xác định giá trị của m để các đa thức sau là tam thức bậc hai
Giải bài 1 trang 9 SGK Toán 10 tập 2 – Chân trời sáng tạo
Đa thức nào sau đây là tam thức bậc hai?
Giải mục 2 trang 8, 9 SGK Toán 10 tập 2 - Chân trời sáng tạo
Quan sát đồ thị của các hàm số bậc hai trong các hình thức dưới đây. Trong mỗi trường hợp, hãy cho biết: Xét dấu của các tam thức bậc hai sau: trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu
Giải mục 1 trang 6, 7 SGK Toán 10 tập 2 - Chân trời sáng tạo
Đồ thị của hàm số y= f(x) được biểu diễn trong hình 1 Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x=1 Tìm biệt thức và nghiệm của các tam thức bậc hai sau:
Lý thuyết Dấu của tam thức bậc hai - SGK Toán 10 Chân trời sáng tạo
A. Lý thuyết 1. Tam thức bậc hai