Giải bài 24 trang 14 sách bài tập toán 12 - Cánh diều

Trong một thí nghiệm y học, người ta cấy 1 000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: $N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}$ trong đó $t$ là thời gian tính bằng giây $\left( {t \ge 0} \right)$ (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Trong khoảng thời gian nào từ lúc nuôi cấy, số lượng vi khuẩn sẽ tăng lên?

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Trong một thí nghiệm y học, người ta cấy 1 000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức:

$N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}$

trong đó $t$ là thời gian tính bằng giây $\left( {t \ge 0} \right)$ (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Trong khoảng thời gian nào từ lúc nuôi cấy, số lượng vi khuẩn sẽ tăng lên?

Phương pháp giải - Xem chi tiết

Xét hàm số $N\left( t \right)$ trên nửa khoảng $\left[ {0; + \infty } \right)$, lập bảng biến thiên và tìm khoảng đồng biến của hàm số.

Lời giải chi tiết

Xét hàm số $N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}$ trên nửa khoảng $\left[ {0; + \infty } \right)$.

Ta có:

$N'\left( t \right) = \frac{{{{\left( {100t} \right)}^\prime }\left( {100 + {t^2}} \right) - \left( {100t} \right){{\left( {100 + {t^2}} \right)}^\prime }}}{{{{\left( {100 + {t^2}} \right)}^2}}} = \frac{{100\left( {100 + {t^2}} \right) - \left( {100t} \right).2t}}{{{{\left( {100 + {t^2}} \right)}^2}}} = \frac{{ - 100{t^2} + 10000}}{{{{\left( {100 + {t^2}} \right)}^2}}}$

$N'\left( t \right) = 0$ khi hoặc $t = 10$.

Bảng biến thiên của hàm số:

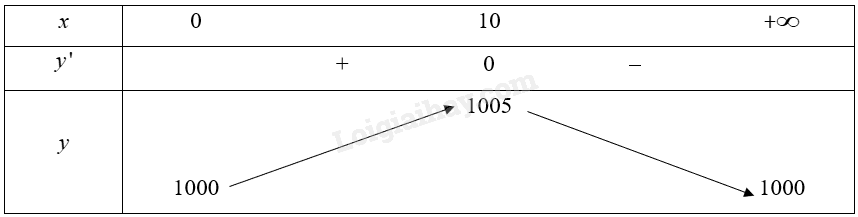
Vậy hàm số đồng biến trên khoảng $\left( {0;10} \right)$.

Vậy trong khoảng thời gian từ 0 giây đến 10 giây, số lượng vi khuẩn sẽ tăng lên.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 25 trang 15 sách bài tập toán 12 - Cánh diều
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình $s\left( t \right) = {t^3} - 6{t^2} + 14t + 1$ trong đó $t$ tính bằng giây và $s$ tính bằng mét. Trong khoảng thời gian nào của 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên?
Giải bài 23 trang 14 sách bài tập toán 12 - Cánh diều
Tìm điểm cực trị của mỗi hàm số sau: a) (y = x.{e^x}); b) (y = {left( {x + 1} right)^2}.{e^{ - x}}); c) (y = {x^2}.ln {rm{x}}); d) (y = frac{x}{{ln {rm{x}}}}).
Giải bài 22 trang 14 sách bài tập toán 12 - Cánh diều
Chứng minh rằng: a) Hàm số $y = \sqrt {{x^2} - 4} $ nghịch biến trên khoảng $\left( { - \infty ; - 2} \right)$ và đồng biến trên khoảng $\left( {2; + \infty } \right)$. b) Hàm số $y = \ln \left( {{x^2} + 1} \right)$ nghịch biến trên khoảng $\left( { - \infty ;0} \right)$ và đồng biến trên khoảng $\left( {0; + \infty } \right)$. c) Hàm số $y = {2^{ - {x^2} + 2x}}$ đồng biến trên khoảng $\left( { - \infty ;1} \right)$ và nghịch biến trên khoảng $\left( {1; + \infty } \right)$.
Giải bài 21 trang 14 sách bài tập toán 12 - Cánh diều
Dùng đạo hàm của hàm số, hãy giải thích: a) Hàm số $y = {a^x}$ đồng biến trên $\mathbb{R}$ khi $a > 1$, nghịch biến trên $\mathbb{R}$ khi $0 < a < 1$. b) Hàm số $y = {\log _a}x$ đồng biến trên khoảng $\left( {0; + \infty } \right)$ khi $a > 1$, nghịch biến trên khoảng $\left( {0; + \infty } \right)$ khi $0 < a < 1$.
Giải bài 20 trang 14 sách bài tập toán 12 - Cánh diều
Tìm điểm cực trị của mỗi hàm số sau: a) $y = {x^3} - 12{\rm{x}} + 8$; b) $y = 2{{\rm{x}}^4} - 4{{\rm{x}}^2} - 1$; c) $y = \frac{{{x^2} - 2{\rm{x}} - 2}}{{x + 1}}$; d) $y = - x + 1 - \frac{9}{{x - 2}}$
Giải bài 19 trang 14 sách bài tập toán 12 - Cánh diều
Tìm các khoảng đơn điệu của mỗi hàm số sau: a) $y = - \frac{1}{3}{x^3} + {x^2} + 3{\rm{x}} - 1$; b) $y = {x^3} - 3{x^2} + 3{\rm{x}} - 1$; c) $y = {x^4} + {x^2} - 2$; d) $y = - {x^4} + 2{{\rm{x}}^2} - 1$; e) $y = \frac{{2{\rm{x}} - 3}}{{{\rm{x}} - 4}}$; g) $y = \frac{{{x^2} + x + 2}}{{x + 2}}$.
Giải bài 18 trang 13 sách bài tập toán 12 - Cánh diều
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và đồ thị hàm số $y = f'\left( x \right)$ như Hình 8. a) $f'\left( x \right) = 0$ khi $x = 0,x = 1,x = 3$. b) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( { - \infty ;0} \right)$. c) $f'\left( x \right) > 0$ khi $x \in \left( {0;3} \right)$. d) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {0;3} \right)$.
Giải bài 17 trang 13 sách bài tập toán 12 - Cánh diều
Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số (y = {x^3} - 3{rm{x}} + 2). a) (y' = 3{{rm{x}}^2} - 3). b) (y' = 0) khi (x = - 1,x = 1). c) (y' > 0) khi (x in left( { - 1;1} right)) và (y' < 0) khi (x in left( { - infty ; - 1} right) cup left( {1; + infty } right)). d) Giá trị cực đại của hàm số là ${{f}_{CĐ}}=0$.
Giải bài 16 trang 13 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ và đồ thị hàm số $y = f'\left( x \right)$ như Hình 7. Số điểm cực trị của hàm số $y = f\left( x \right)$ là: A. 4. B. 3. C. 2. D. 1.
Giải bài 15 trang 13 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là: A. 2. B. 1. C. ‒1. D. 0.
Giải bài 14 trang 12 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như Hình 5. Số điểm cực trị của hàm số đã cho là: A. 2. B. 4. C. 1. D. 3.
Giải bài 13 trang 12 sách bài tập toán 12 - Cánh diều
Hàm số $y = {x^3} - 3{x^2} - 9x - 3$ đạt cực tiểu tại điểm: A. ‒1. B. 3. C. 2. D. ‒30.
Giải bài 12 trang 12 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = 2{x^3} + 3x + 2$. Kết luận nào sau đây là đúng? A. Hàm số có 3 cực trị. B. Hàm số có 2 cực trị. C. Hàm số có 1 cực trị. D. Hàm số không có cực trị.
Giải bài 11 trang 12 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = {x^2}{\left( {{x^2} - 1} \right)^2}\left( {x - 2} \right),\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là: A. 1. B. 2. C. 3. D. 4.
Giải bài 10 trang 12 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau: Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại $x = - 5$. B. Hàm số có giá trị cực đại bằng 0. C. Hàm số đạt cực tiểu tại $x = 2$. D. Hàm số đạt cực đại tại $x = 4$.
Giải bài 8 trang 11 sách bài tập toán 12 - Cánh diều
Cho hàm số (y = fleft( x right)) có đạo hàm trên (mathbb{R}) và bảng xét dấu của đạo hàm như sau: Số điểm cực trị của hàm số đã cho là: A. 0. B. 1. C. 2. D. 3.
Giải bài 9 trang 12 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau: Điểm cực đại của hàm số đã cho là: A. ‒1. B. 3. C. 2. D. 0.
Giải bài 7 trang 11 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như Hình 4. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Giải bài 6 trang 11 sách bài tập toán 12 - Cánh diều
Trong các hàm số sau, hàm số đồng biến trên $\mathbb{R}$ là:
Giải bài 5 trang 11 sách bài tập toán 12 - Cánh diều
Cho hàm số (y = frac{x}{{x - 1}}). Mệnh đề nào dưới đây là đúng?
Giải bài 4 trang 11 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = - {x^3} + 3{x^2} - 4$. Mệnh đề nào dưới đây là đúng?
Giải bài 3 trang 10 sách bài tập toán 12 - Cánh diều
Cho hàm số (y = fleft( x right)) có đạo hàm (f'left( x right) = - xleft( {2x - 5} right),forall x in mathbb{R}). Khẳng định nào dưới đây đúng?
Giải bài 2 trang 10 sách bài tập toán 12 - Cánh diều
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
Giải bài 1 trang 10 sách bài tập toán 12 - Cánh diều
Cho hàm số (y = fleft( x right)) có bảng xét dấu của đạo hàm (f'left( x right)) như sau