-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
SBT Toán 11 - giải SBT Toán 11 - Cánh diều
Bài 3. Đường thẳng và mặt phẳng song song - SBT Toán 11..
Giải bài 22 trang 104 sách bài tập toán 11 - Cánh diều
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ACD\), điểm \(M\) nằm trên cạnh \(AB\) sao cho \(AM = 2MB\).
Đã có lời giải SGK Toán lớp 12 - Cánh diều (mới)
Đầy đủ - Chi tiết - Chính xác
Đề bài
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ACD\), điểm \(M\) nằm trên cạnh \(AB\) sao cho \(AM = 2MB\). Đường thẳng \(MG\) song song với mặt phẳng:
A. \(\left( {ACD} \right)\)
B. \(\left( {ABD} \right)\)
C. \(\left( {BCD} \right)\)
D. \(\left( {ABC} \right)\)
Phương pháp giải - Xem chi tiết
Sử dụng dấu hiệu nhận biết đường thẳng song song với mặt phẳng.
Lời giải chi tiết
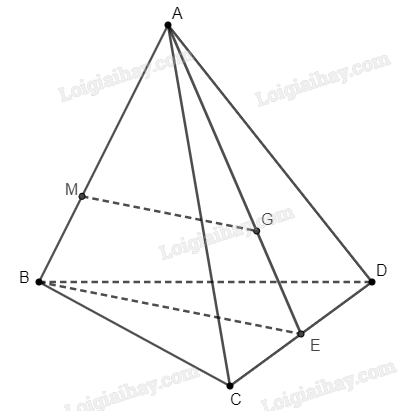
Do \(AM = 2MB \Rightarrow \frac{{AM}}{{AB}} = \frac{2}{3}\).
Gọi \(E\) là trung điểm của \(CD\). Do \(G\) là trọng tâm tam giác \(ACD\), ta suy ra ba điểm \(A\), \(G\), \(E\) thẳng hàng và \(\frac{{AG}}{{AE}} = \frac{2}{3}\).
Tam giác \(ABE\) có \(\frac{{AM}}{{AB}} = \frac{{AG}}{{AE}}\) nên theo định lí Thales đảo, \(GM\parallel BE\).
Mà \(BE \subset \left( {BCD} \right)\), ta suy ra \(GM\parallel \left( {BCD} \right)\).
Đáp án đúng là C.
Bình luận
Chia sẻ
- Giải bài 23 trang 104 sách bài tập toán 11 - Cánh diều
- Giải bài 24 trang 104 sách bài tập toán 11 - Cánh diều
- Giải bài 25 trang 104 sách bài tập toán 11 - Cánh diều
- Giải bài 26 trang 104 sách bài tập toán 11 - Cánh diều
- Giải bài 27 trang 105 sách bài tập toán 11 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
