Copyright © 2021 loigiaihay.com
Từ điển Toán 11 | Các dạng bài tập Toán 11
Hai mặt phẳng song song - Từ điển môn Toán 11
Hai mặt phẳng song song - Từ điển môn Toán 11 Định lí Thalès trong không gian - Toán 11
1. Định lí Thalès trong không gian
Nếu a, b là hai đường thẳng phân biệt cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\)
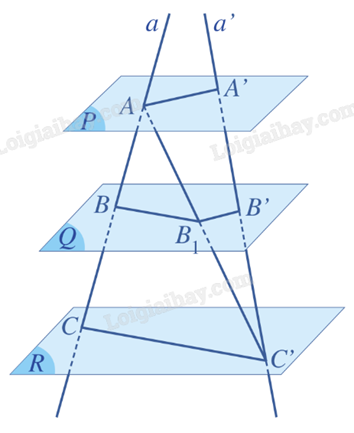
2. Ví dụ minh hoạ về định lí Thalès trong không gian
1) Cho ba mặt phẳng (P), (Q), (R) đôi một song song. Hai đường thẳng d và d' cắt ba mặt phẳng (P), (Q), (R) lần lượt tại A, B, C và A', B', C'. Cho AB = 3, BC = 7, A'C' = 20. Tính các độ dài A'B', B'C'.
Giải:
Áp dụng định lí Thales trong không gian đối với ba mặt phẳng song song (P), (Q), (R) và hai cát tuyến d, d', ta có:
\(\frac{{A'B'}}{{B'C'}} = \frac{{AB}}{{BC}} = \frac{3}{7}\), suy ra \(\frac{{A'B'}}{3} = \frac{{B'C'}}{7} = \frac{{A'B' + B'C'}}{{3 + 7}} = \frac{{A'C'}}{{10}} = \frac{{20}}{{10}} = 2\).
Suy ra \(A'B' = 6;B'C' = 14\).
2) Một kệ để đồ bằng gỗ có mâm tầng dưới (ABCD) và mâm tầng trên (EFGH) song song với nhau. Bác thợ mộc đo được AE = 80 cm, CG = 90 cm và muốn đóng thêm một mâm tầng giữa (IJKL) song song với hai mâm tầng trên và dưới sao cho khoảng cách EI = 36 cm. Hãy giúp bác thợ mộc tính độ dài GK để đặt mâm tầng giữa cho kệ để đồ đúng vị trí.
Giải:
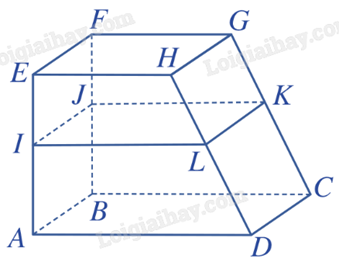
Ta có đường thẳng EA cắt ba mặt phẳng song song (EFGH), (IJKL), (ABCD) lần lượt tại E, I, A; đường thẳng GC cũng cắt ba mặt phẳng trên lần lượt tại G, K, C.
Áp dụng định lí Thales trong không gian, ta có: \(\frac{{EI}}{{EA}} = \frac{{GK}}{{GC}} \Rightarrow \frac{{36}}{{80}} = \frac{{GK}}{{90}}\).
Suy ra \(GK = \frac{{90.36}}{{80}} = 40,5\) (cm).
Vậy độ dài GK = 40,5 cm.
3) Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm \({A_1},{A_2}\) sao cho \({A_2}{A_1} = 2{A_1}A\). Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua \({A_1},{A_2}\). Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại \({B_1},{C_1}\). Mặt phẳng (Q) cắt các cạnh SB, SC lần lượt tại \({B_2},{C_2}\). Chứng minh \({B_2}{B_1} = 2{B_1}B\) và \({C_2}{C_1} = 2{C_1}C\).
Giải:
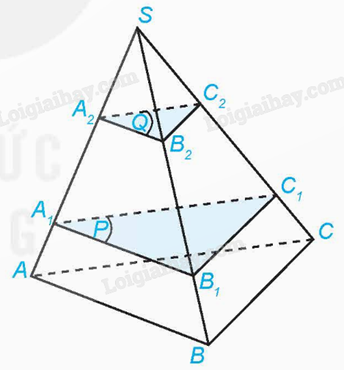
Áp dụng định lí Thales cho ba mặt phẳng đôi một song song (P), (Q), (ABC) và hai cát tuyến SA, SB, ta có:
\(\frac{{{A_2}{A_1}}}{{{A_1}A}} = \frac{{{B_2}{B_1}}}{{{B_1}B}}\).
Vì \({A_2}{A_1} = 2{A_1}A\) nên \({B_2}{B_1} = 2{B_1}B\).
Tương tự với hai cát tuyến SA, SC suy ra \({C_2}{C_1} = 2{C_1}C\).
