1. Định nghĩa phép chiếu song song
Trong không gian, cho mặt phẳng (P) và đường thẳng \(l\) cắt (P). Với mỗi điểm M trong không gian, vẽ một đường thẳng đi qua M và song song hoặc trùng với \(l\). Đường thẳng này cắt (P) tại M’. Phép cho tương ứng mỗi điểm M trong không gian với điểm M’ trong (P) được gọi là phép chiếu song song lên mặt phẳng (P) theo phương \(l\).
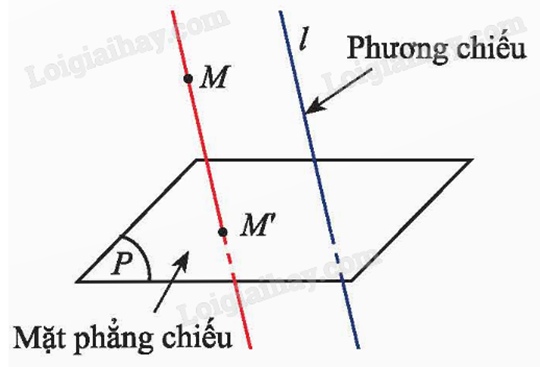
+ Mặt phẳng (P) được gọi là mặt phẳng chiếu và đường thẳng \(l\) được gọi là phương chiếu của phép chiếu song song nói trên.
+ Phép chiếu song song theo phương \(l\) còn được gọi tắt là phép chiếu theo phương \(l\).
+ Điểm M’ gọi là ảnh của điểm M qua phép chiếu theo phương \(l\).
+ Cho hình H trong không gian. Ta gọi tập hợp H’ các ảnh M’ của tất cả những điểm M thuộc H qua phép chiếu song song theo phương \(l\) là hình chiếu song song của H lên mặt phẳng (P).
2. Các tính chất cơ bản của phép chiếu song song
- Hình chiếu song song của một đường thẳng là một đường thẳng. Hình chiếu song song của một đoạn thẳng là một đoạn thẳng. Hình chiếu song song của một tia là một tia.
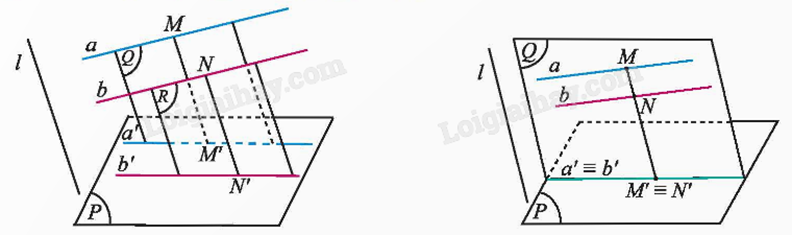
- Hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song.
- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
- Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau.
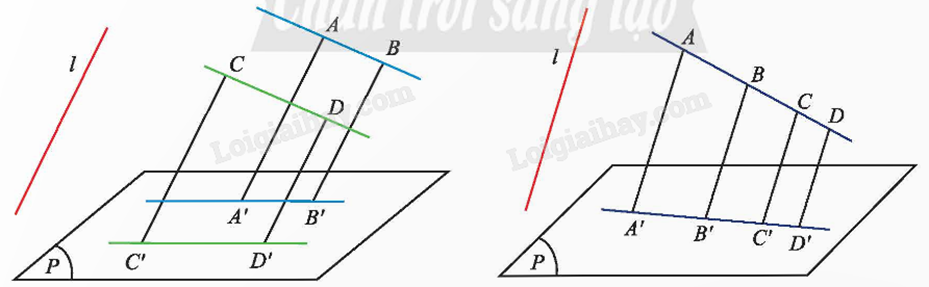
3. Khái niệm hình biểu diễn của một hình không gian
Hình biểu diễn của một hình H trong không gian là hình chiếu song song của hình H trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
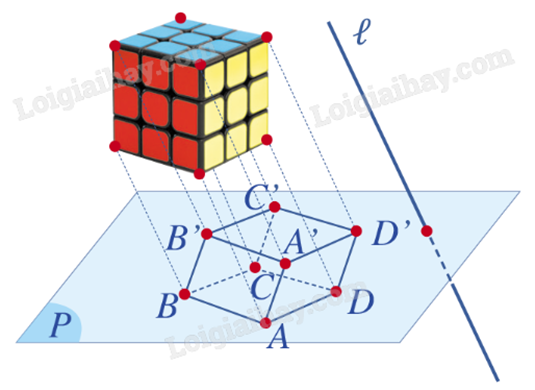
Chú ý: Muốn vẽ đúng hình biểu diễn của hình không gian, ta phải áp dụng các tính chất của phép chiếu song song.
Ví dụ minh hoạ:
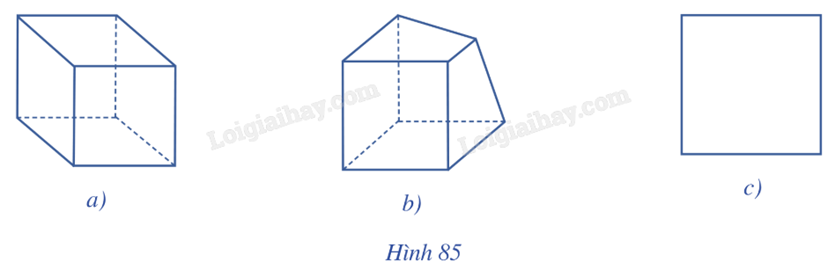
Trong các Hình 85a, 85b, 85c, hình nào biểu diễn cho hình lập phương?
Giải:
Hình 85a là hình biểu diễn của hình lập phương.
Hình 85b không là hình biểu diễn của hình lập phương vì trong hình này có hai cạnh đối của đáy trên không song song với nhau.
Hình 85c cũng có thể là hình biểu diễn của hình lập phương. Tuy nhiên hình biểu diễn này không tốt vì không giúp ta hình dung được hình trong không gian.
4. Hình biểu diễn của một số hình khối đơn giản
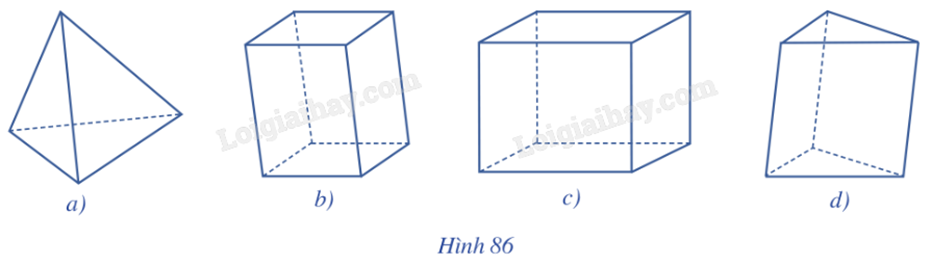
Các hình sau đây được sử dụng làm hình biểu diễn của: hình tử diện (Hình 86a); hình hộp (Hình 86b); hình hộp chữ nhật (Hình 86c); hình lăng trụ tam giác (Hình 86d).
- Một tam giác bất kỳ bao giờ cũng có thể coi là hình biểu diễn của một tam giác có dạng tuỳ ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông, ...).
- Một hình bình hành bất kỳ bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành tuỳ ý cho trước (có thể là hình bình hành, hình vuông, hình thoi, hình chữ nhật, ...).
- Một hình thang bất kỳ bao giờ cũng có thể coi là hình biểu diễn cho một hình thang tuỳ ý cho trước, sao cho tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.
- Ta thường dùng đường elip làm hình biểu diễn của đường tròn, của hình elip biểu diễn cho tâm của đường tròn.
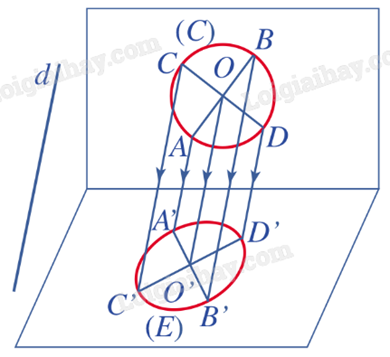
- Phép chiếu song song nói chung không giữ nguyên tỉ số của hai đoạn thẳng không nằm trên hai đường thẳng song song (hay không cùng nằm trên một đường thẳng) và không giữ nguyên độ lớn của một góc. Từ đó suy ra nếu trên hình H có hai đoạn thẳng không nằm trên hai đường thẳng song song thì tỉ số của chúng không nhất thiết phải giữ nguyên trên hình biểu diễn. Cũng như vậy, độ lớn của một góc trên hình H không nhất thiết được giữ nguyên trên hình biểu diễn.

 Phép chiếu song song - Từ điển môn Toán 11
Phép chiếu song song - Từ điển môn Toán 11 





