Đề thi học kì 1 Toán 7 - Đề số 8 - Kết nối tri thức

Đề bài

Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Nếu  \(\sqrt x  = 4\) thì  x bằng

     A. 2                                    B. 4                                    C. \( \pm \)2                 D. 16

Câu 2: Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau:

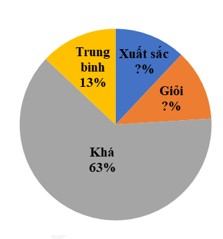
Tìm tỉ số phần trăm số học sinh xuất sắc và số hóc inh giỏi của lớp đó, biết rằng số học sinh xuất sắc bằng số học sinh giỏi.

     A. Số học sinh xuất sắc chiếm \(14\% \), số học sinh giỏi chiếm \(14\% \).                   

     B. Số học sinh xuất sắc chiếm \(16\% \), số học sinh giỏi chiếm \(16\% \).                   

     C. Số học sinh xuất sắc chiếm \(15\% \), số học sinh giỏi chiếm \(15\% \).                   

     D. Số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \).

Câu 3: Trong các phân số sau đây, phân số nào biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{2}\).

     A. \(\dfrac{{ - 2}}{4}\)          B. \(\dfrac{{ - 22}}{{48}}\)    C. \( - \dfrac{{ - 5}}{{10}}\)   D. \(\dfrac{{ - 6}}{{18}}\)

Câu 4: Cách viết nào dưới đây là đúng?

     A. \(\left| { - 0,55} \right| = 0,55\)                                  B. \(\left| {0,55} \right| =  - 0,55\)   C. \(\left| { - 0,55} \right| =  - 0,55\)             D. \( - \left| {0,55} \right| = 0,55\)

Câu 5: Cho \(x = 6,67254\). Khi làm tròn đến chữ số thập phân thứ ba thì được kết quả là:

     A. \(6,672\)                        B. \(6,672\)                        C. \(6,67\)                     D. \(6,6735\)

Câu 6: Kết quả của phép tính:  \({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3}\)bằng:

     A. \({\left( {\dfrac{1}{2}} \right)^2}.\)                             B. \({\left( {\dfrac{1}{2}} \right)^5}\)           C. \({\left( {\dfrac{1}{2}} \right)^3}\)                                        D. \(\dfrac{1}{2}\)

Câu 7: Nếu \(\Delta ABC = \Delta DEF\) thì điều nào sau đây là không đúng?

     A. \(\angle A = \angle E\)    B. \(AB = DE\)                          C. \(BC = EF\)                          D. \(\angle C = \angle F\)

Câu 8: Cho a\( \bot \)b và b\( \bot \)c thì:

     A. a // b                              B. a // c                              C. b // c                         D. a // b // c

Câu 9:  Tam giác MNP có \(\angle M = {60^0}\), \(\angle N = {20^0}\), NK là tia phân giác. Số đo của góc \(\widehat {NKP}\) bằng:

     A. 110                                B. 100                                C. 70                             D. 30

Câu 10: Cho biểu đồ thể hiện tỉ lệ gia tăng dân số Việt Nam từ năm 1991 đến năm 2019 như dưới đây:

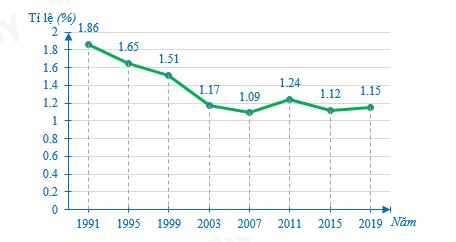
Tỉ lệ gia tăng dân số giai đoạn 1991 - 2007 tăng (hay giảm) bao nhiêu phần trăm?

     A. Tăng 0,77%;                 B. Giảm 0,77%;                 C. Tăng 0,17%;                 D. Giảm 0,17%.

Phần II: Tự luận (7 điểm).

Câu 1: (2 điểm) Thực hiện phép tính:

a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)                                               b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right).\)                   

c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0}\).                    d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}}  - {2^2}.\left| { - \dfrac{1}{4}} \right|\)

Câu 2: (1,5 điểm) Tìm x

     a. \(\,x + 1\dfrac{1}{2} =  - 5,6\)                                                b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4}\)                                    c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4}\)

Câu 3: (3 điểm) Cho tam giác \(ABC\) vuông tại \(A\). Kẻ tia phân giác của \(\angle ABC\) cắt cạnh \(AC\) tại \(M\). Trên cạnh \(BC\) lấy điểm \(N\) sao cho \(BN = BA.\)

1) Chứng minh: \(\Delta BAM = \Delta BNM\).

2) Gọi \(I\) là giao điểm của \(BM\) và \(AN\). Chứng minh \(I\) là trung điểm của đoạn thẳng \(AN\).

3) Trên tia đối của tia \(AB\) lấy điểm \(K\) sao cho \(AK = NC\). Chứng minh \(\angle ABC = \angle NMC\) và \(K,M,N\) là ba điểm thẳng hàng.

Câu 4: (0,5 điểm) So sánh \({2^{30}} + {3^{30}} + {4^{30}}\) và \({3.24^{10}}\)

Lời giải

I. Phần trắc nghiệm (3 điểm)

Câu 1

Phương pháp:

Chỉ tồn tại căn bậc hai số học của số x không âm.

Cách giải:

\(\sqrt x  = 4 \Leftrightarrow x = 16\)

Chọn D.

Câu 2

Phương pháp:

Đọc và phân tích dữ liệu của biểu đồ hình quạt tròn.

Cách giải:

Gọi số phần trăm học sinh xuất sắc là \(x\% \) (điều kiện: \(x > 0\)). Vì số học sinh xuất sắc bằng số học sinh giỏi nên số phần trăm học sinh giỏi là \(x\% \) (điều kiện: \(x > 0\)).

Ta có:

\(\begin{array}{l}x + x + 63\%  + 13\%  = 100\% \\2x + 76\%  = 100\% \\2x = 100\%  - 76\% \\2x = 24\% \\x = 24\% :2\\x = 12\% \end{array}\)

Vậy số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \).

Chọn D.

Câu 3

Phương pháp:

Số đối của a là - a

Cách giải:

Số đối của \(\dfrac{{ - 1}}{2}\) là \(\dfrac{1}{2} =  - \dfrac{{ - 5}}{{10}}\)

Chọn C.

Câu 4

Phương pháp:

\(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,khi\,\,x \ge 0\\ - x\,\,khi\,\,x < 0\end{array} \right.\)

Cách giải:

\(\left| { - 0,55} \right| = 0,55\)

Chọn A.

Câu 5

Phương pháp:

So sánh số thập phân thứ 4 với số 5.

Cách giải:

Số thập phân thứ 3 là 2 và số thập phân thứ 4 là số 5 nên kết quả làm tròn bằng 6,672

Chọn B.

Câu 6

Phương pháp:

\({a^m}.{a^n} = {a^{m + n}}\)

Cách giải:

\({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3} = {\left( {\dfrac{1}{2}} \right)^{2 + 3}} = {\left( {\dfrac{1}{2}} \right)^5}\)

Chọn B.

Câu 7

Phương pháp:

Vận dụng định nghĩa của hai tam giác bằng nhau.

Cách giải:

\(\Delta ABC = \Delta DEF \Rightarrow \angle A = \angle D\) do đó, đáp án A không đúng.

Chọn A.

Câu 8

Phương pháp:

Định lý từ vuông góc đến song song

Cách giải:

Vì a và c cùng vuông góc với b nên ta suy ra a // c.

Chọn B.

Câu 9

Phương pháp:

Dùng tính chất của tia phân giác

Cách giải:

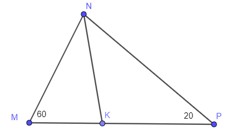
 \(\begin{array}{l}\angle MNP = {180^0} - \angle N - \angle P = 180 - 60 - 20 = 100\\ \Rightarrow \angle MNK = 100:2 = 50\\ \Rightarrow \angle MKN = \angle M + \angle MNK = 60 + 50 = 110\end{array}\)

Chọn A.

Câu 10

Phương pháp:

Quan sát biểu đồ và xem tỉ lệ gia tăng dân số mỗi năm.

Cách giải:

Tỉ lệ gia tăng dân số Việt Nam năm 1991, 1995, 1999, 2003, 2007 lần lượt là: 1,86%; 1,65%; 1,51%; 1,17%; 1,09%

Ta có 1,86% < 1,65% < 1,51% < 1,17% < 1,09%

Do đó tỉ lệ gia tăng dân số Việt Nam giai đoạn 1991 – 2007 giảm:

1,86% – 1,09% = 0,77%

Chọn B.

II. Phần tự luận (7 điểm)

Câu 1

Phương pháp:

Áp dụng tính toán theo thứ tự thực hiện phép tính.

Cách giải:

a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\)\( = \dfrac{{2 + ( - 17) + 8}}{7} = \dfrac{{ - 7}}{7} =  - 1\)

b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right) = \dfrac{5}{9}:\dfrac{{ - 3}}{{22}} + \dfrac{5}{9}:\dfrac{{ - 3}}{5} = \dfrac{5}{9}.\dfrac{{ - 22}}{3} + \dfrac{5}{9}.\dfrac{{ - 5}}{3}\)

\( = \left( {\dfrac{{ - 22}}{3} + \dfrac{{ - 5}}{3}} \right).\dfrac{5}{9} = ( - 9).\dfrac{5}{9} =  - 5\)

c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0} = \dfrac{{ - 8}}{5}.\left| {\dfrac{{ - 3}}{4}} \right| + 1\)\( = \dfrac{{ - 8}}{5}.\dfrac{3}{4} + 1 = \dfrac{{ - 6}}{5} + 1 = \dfrac{{ - 1}}{5}\)

d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}}  - {2^2}.\left| { - \dfrac{1}{4}} \right|\)=\( - \dfrac{5}{2}.\dfrac{3}{5} - 4.\dfrac{1}{4}\)=\( - \dfrac{3}{2} - 1\)=\( - \dfrac{5}{2}\)

Câu 2

Phương pháp:

\(\left| x \right| = a\,\) với \((a > 0)\)\( \Leftrightarrow \left[ \begin{array}{l}x = a\\x =  - a\end{array} \right.\)

\({x^2} = a\,\)với \((a > 0)\) \( \Leftrightarrow \left[ \begin{array}{l}x = \sqrt a \\x =  - \sqrt a \end{array} \right.\)

Cách giải:

a. \(x + 1\dfrac{1}{2} =  - 5,6 \Leftrightarrow x + 1,5 =  - 5,6 \Leftrightarrow x =  - 5,6 - 1,5 \Leftrightarrow x = \, - 7,1\)

b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4} \Rightarrow \left[ \begin{array}{l}x - \dfrac{1}{4} = \dfrac{5}{4}\\x - \dfrac{1}{4} =  - \dfrac{5}{4}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\, = \dfrac{3}{2}\\x\,\,\,\,\,\,\,\,\,\,\, =  - 1\end{array} \right.\)

c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4} \Rightarrow \left[ \begin{array}{l}\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{3}{2}\\\dfrac{1}{5} - \dfrac{3}{2}x = \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{3}{2}\\\dfrac{3}{2}x = \dfrac{1}{5} - \dfrac{{ - 3}}{2}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\dfrac{3}{2}x = \dfrac{{ - 13}}{{10}}\\\dfrac{3}{2}x = \dfrac{{17}}{{10}}\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{{ - 13}}{{15}}\\x = \dfrac{{17}}{{15}}\end{array} \right.\)

Câu 3

Phương pháp:

1) Chứng minh \(\Delta BAM = \Delta BNM\left( {c.g.c} \right)\)

2) Chứng minh \(BM\) là đường trung trực của đoạn thẳng \(AN\)

Mà \(I\) là giao điểm của \(BM\) và \(AN\) nên \(I\) là trung điểm của \(AN\).

3) *Chứng minh \(\angle MNC = {90^0}\)

Ta có: \(\left\{ \begin{array}{l}\angle ABC + \angle ACB = \angle BAC = {90^0}\\\angle MCN + \angle CMN = \angle MNC = {90^0}\end{array} \right.\), suy ra \(\angle ABC = \angle CMN\) (đpcm)

*Chứng minh \(\Delta MAK = \Delta MNC\left( {c.g.c} \right) \Rightarrow \angle AMK = \angle CMN\)

\( \Rightarrow \angle AMN + \angle AMK = {180^0}\)

Do đó, \(K,M,N\) là ba điểm thẳng hàng.

Cách giải:

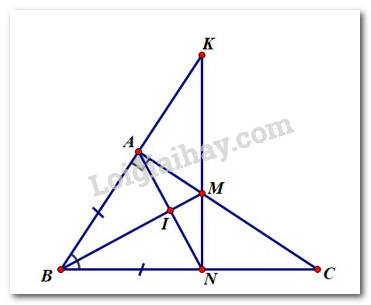
1) Vì \(BM\) là phân giác của \(\angle ABC \Rightarrow \angle ABM = \angle NBM\)

Xét \(\Delta BAM\) và \(\Delta BNM\) có:

\(\left. \begin{array}{l}AB = BN\left( {gt} \right)\\\angle ABM = \angle NBM\left( {cmt} \right)\\BM\,\,chung\end{array} \right\} \Rightarrow \Delta BAM = \Delta BNM\left( {c.g.c} \right)\)

2) \(\Delta BAM = \Delta BNM\left( {cmt} \right) \Rightarrow AM = MN\) (hai cạnh tương ứng)

Ta có: \(AB = BN\left( {gt} \right)\) và \(AM = MN\left( {cmt} \right)\)

\( \Rightarrow BM\) là đường trung trực của đoạn thẳng \(AN\)

Mà \(I\) là giao điểm của \(BM\) và \(AN\) nên \(I\) là trung điểm của \(AN\).

3) *\(\Delta ABC\) vuông tại \(A\left( {gt} \right) \Rightarrow \angle BAC = {90^0}\) hay \(\angle BAM = {90^0}\)

\(\Delta BAM = \Delta BNM\left( {cmt} \right) \Rightarrow \angle BAM = \angle BNM = {90^0}\)

Hai góc \(\angle BNM\) và \(\angle MNC\) kề bù nhau nên \(\angle MNC = {180^0} - {90^0} = {90^0}\)

Ta có: \(\left\{ \begin{array}{l}\angle ABC + \angle ACB = \angle BAC = {90^0}\\\angle MCN + \angle CMN = \angle MNC = {90^0}\end{array} \right.\), suy ra \(\angle ABC = \angle CMN\) (đpcm)

*Xét \(\Delta MAK\) và \(\Delta MNC\) có:

\(\left. \begin{array}{l}AM = MN\left( {cmt} \right)\\\angle KAM = \angle MNC = {90^0}\\AK = NC\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta MAK = \Delta MNC\left( {c.g.c} \right) \Rightarrow \angle AMK = \angle CMN\) (hai góc tương ứng)

Ta có: \(\angle AMN + \angle CMN = {180^0}\) mà \(\angle CMN = \angle AMK\left( {cmt} \right)\)

\( \Rightarrow \angle AMN + \angle AMK = {180^0}\)

Do đó, \(K,M,N\) là ba điểm thẳng hàng.

Câu 4

Phương pháp:

Đưa về lũy thừa cùng cơ số hoặc cùng số mũ để so sánh.

Cách giải:

Ta có: \({4^{30}} = {2^{30}}{.2^{30}} = {\left( {{2^3}} \right)^{30}}.{\left( {{2^2}} \right)^{15}} > {8^{10}}{.3^{15}} > \left( {{8^{10}}{{.3}^{10}}} \right).3 > {24^{10}}.3\)                  

Vậy \({2^{30}} + {3^{30}} + {4^{30}}\) > \({3.24^{10}}\).