 Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
 Đề thi giữa kì 1 Toán 7 Kết nối tri thức
Đề thi giữa kì 1 Toán 7 Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 5 - Kết nối tri thức
Tải vềPhần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Tìm phát biểu đúng trong các phát biểu sau:
A. \(\dfrac{2}{5} \in \mathbb{Z}\)
B. \( - 5 \in \mathbb{N}\)
C. \(\dfrac{{ - 5}}{4} \notin \mathbb{Q}\)
D. \(\dfrac{3}{2} \in \mathbb{Q}\)
Câu 2: Tìm \(x\), biết: \(\dfrac{1}{2} - \dfrac{2}{3}x = \dfrac{1}{4}\)
A. \(x = \dfrac{{ - 3}}{8}\)
B. \(x = \dfrac{3}{8}\)
C. \(x = \dfrac{1}{2}\)
D. \(x = - 1\)
Câu 3: Kết quả của phép tính: \(\sqrt {1,44} - 2.{\left( {\sqrt {0,6} } \right)^2}\)
A. \(0,24\)
B. \(0\)
C. \(0,12\)
D. \(0,2\)
Câu 4: Cho hình vẽ. Chọn câu đúng nhất:
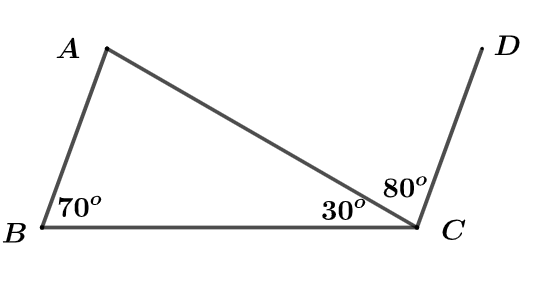
A. \(\angle A = {80^o}\)
B. \(AB\,//\,CD\)
C. Cả A và B đều đúng
D. A đúng, B sai
Câu 5: Vẽ hai đoạn thẳng \(AA',\,CC'\) cắt nhau tại \(B\) sao cho \(\angle A'BC = {47^o}.\) Số đo các góc \(\angle ABC',\,\angle ABC,\,\angle A'BC'\) lần lượt bằng?
A. \({47^o},\,{133^o},\,{133^o}\)
B. \({133^o},\,{47^o},\,{133^o}\)
C. \({47^o},\,{180^o},\,{180^o}\)
D.\({57^o},\,{133^o},\,{57^o}\)
Câu 6: Điền cụm từ còn thiếu vào …: “Định lí …”
A. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
B. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
C. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy….
D. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy ….
Phần II. Tự luận (7 điểm):
Bài 1: (2 điểm)
Thực hiện phép tính:
a) \(\dfrac{{13}}{{50}}.\left( { - 15,5} \right) - \dfrac{{13}}{{50}}.84\dfrac{1}{2}\)
b) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.\left( { - 0,5} \right)\)
c) \(4.{\left( { - \dfrac{1}{2}} \right)^3} - 2.{\left( {\dfrac{{ - 1}}{2}} \right)^2} + 3.\left( { - \dfrac{1}{2}} \right) + 1\)
d) \(\dfrac{{{{\left( { - 0,7} \right)}^2}.{{\left( { - 5} \right)}^3}}}{{{{\left( {\dfrac{{ - 7}}{3}} \right)}^3}.{{\left( {\dfrac{3}{2}} \right)}^4}.{{\left( { - 1} \right)}^5}}}\)
Bài 2: (2 điểm)
Tìm \(x\), biết:
a) \({\left( {\dfrac{4}{5}} \right)^6}.x = {\left( {\dfrac{4}{5}} \right)^7}\)
b) \({\left( {0,03} \right)^3}:x = - {\left( {0,03} \right)^2}\)
c) \(\sqrt {0,16} + x = 3.\sqrt {0,09} .2\dfrac{1}{3}\)
d) \(\sqrt {0,25} - 3x - \sqrt {0,49} .\dfrac{1}{7} = \sqrt {0,04} .\dfrac{1}{2}\)
Bài 3: (1 điểm)
Cho góc vuông \(uOv\) và tia \(Oy\) đi qua một điểm trong của góc đó. Vẽ tia \(Ox\) sao cho \(Ou\) là tia phân giác của góc \(xOy\). Vẽ tia \(Oz\) sao cho \(Ov\) là tia phân giác của góc \(yOz\). Chứng minh rằng hai góc \(xOy\) và \(yOz\) là hai góc kề bù.
Bài 4: (1,5 điểm)
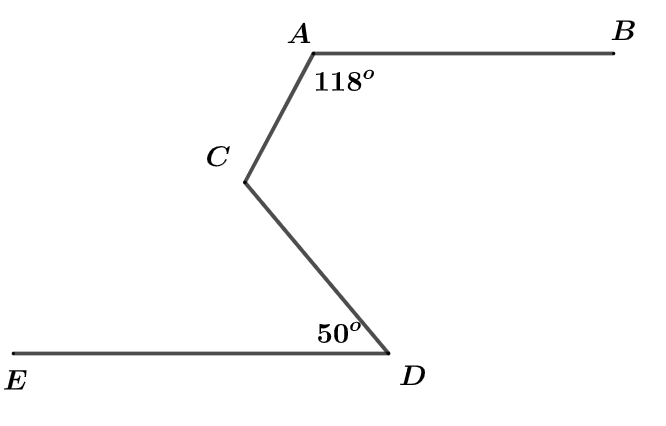
Cho hình vẽ, biết \(AB\,//\,ED,\,\angle BAC = {118^o},\,\angle CDE = {50^o}.\) Hãy tính số đo góc \(\angle ACD.\)
Bài 5: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức: \(A = \dfrac{{2{{\left( {2x + 1} \right)}^2}}}{5} - {2023^0}\)
Lời giải
Phần I: Trắc nghiệm
|
1.D |
2.B |
3.B |
4.C |
5.A |
6.A |
Câu 1:
Phương pháp:
Tập hợp các số tự nhiên được kí hiệu là: \(\mathbb{N}\)
Tập hợp các số nguyên được kí hiệu là: \(\mathbb{Z}\)
Tập hợp các số hữu tỉ được kí hiệu là: \(\mathbb{Q}\).
Cách giải:
+ \(\dfrac{2}{5} \in \mathbb{Z}\) là sai vì \(\dfrac{2}{5} \in \mathbb{Q}\) nên loại đáp án A.
+ \( - 5 \in \mathbb{N}\) là sai vì \( - 5 \in \mathbb{Z}\) hoặc \( - 5 \in \mathbb{Q}\) nên loại đáp án B.
+ \(\dfrac{{ - 5}}{4} \notin \mathbb{Q}\) là sai vì \(\dfrac{{ - 5}}{4} \in \mathbb{Q}\) nên loại đáp án C.
+ \(\dfrac{3}{2} \in \mathbb{Q}\) là đúng nên chọn đáp án D.
Chọn D.
Câu 2:
Phương pháp:
Vận dụng quy tắc chuyển vế tìm giá trị của \(x\).
Cách giải:
\(\dfrac{1}{2} - \dfrac{2}{3}x = \dfrac{1}{4}\)
\(\begin{array}{l}\dfrac{2}{3}x = \dfrac{1}{2} - \dfrac{1}{4}\\\dfrac{2}{3}x = \dfrac{2}{4} - \dfrac{1}{4}\\\dfrac{2}{3}x = \dfrac{{1}}{4}\\x = \dfrac{{ 1}}{4}:\dfrac{2}{3}\\x = \dfrac{{ 1}}{4}.\dfrac{3}{2}\\x = \dfrac{{ 3}}{8}\end{array}\)
Vậy \(x = \dfrac{{ 3}}{8}\)
Chọn B.
Câu 3:
Phương pháp:
Thực hiện tính toán với biểu thức có chứa căn bậc hai.
Cách giải:
\(\sqrt {1,44} - 2.{\left( {\sqrt {0,6} } \right)^2}\)
\(\begin{array}{l} = 1,2 - 2.0,6\\ = 1,2 - 1,2\\ = 0\end{array}\)
Chọn B.
Câu 4:
Phương pháp:
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau.
- Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt đường thẳng phân biệt ab, và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng hai thì a và b song song với nhau.
Cách giải:
Xét \(\Delta ABC\) có \(\angle A + \angle B + \angle BCA = {180^o}\) (tổng ba góc trong một tam giác)
\( \Rightarrow \angle A = 180 - \angle B - \angle BCA = {180^o} - {70^o} - {30^o} = {80^o}\) \( \Rightarrow \) Đáp án A đúng
Ta lại có \(\angle A = {80^o} = \angle ACD\)
Mà hai góc này ở vị trí so le trong
\( \Rightarrow AB\,//\,CD \Rightarrow \) Đáp án B đúng
Vậy cả A và B đều đúng.
Chọn C.
Câu 5
Phương pháp:
Hai góc đối đỉnh thì bằng nhau.
Cách giải:
Ta có \(\angle ABC' = \angle A'BC = {47^o}\) (hai góc đối đỉnh)
Mà \(\angle A'BC + \angle ABC = {180^o}\) (hai góc kề bù)
\( \Rightarrow \angle ABC = {180^o} - {47^o} = {133^o} = \angle A'BC'\)
Chọn A.
Câu 6:
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Chọn A.
Phần II. Tự luận:
Bài 1:
Phương pháp:
a), b) Thực hiện phép cộng, trừ nhân chia số hữu tỉ.
c), d) Thực hiện phép tính có lũy thừa của một số hữu tỉ.
Chú ý: \({\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{{{y^n}}}\left( {y \ne 0} \right)\)
\(\dfrac{{{x^m}}}{{{x^n}}} = {x^m}:{x^n} = {x^{m - n}}\)\(\left( {x \ne 0;m,n \in {\mathbb{N}^*}} \right)\)
Cách giải:
a) \(\dfrac{{13}}{{50}}.\left( { - 15,5} \right) - \dfrac{{13}}{{50}}.84\dfrac{1}{2}\)
\(\begin{array}{l} = \dfrac{{13}}{{50}}.\left( { - 15,5 - 84\dfrac{1}{2}} \right)\\ = \dfrac{{13}}{{50}}.\left( {\dfrac{{ - 31}}{2} - \dfrac{{169}}{2}} \right)\\ = \dfrac{{13}}{{50}}.\dfrac{{\left( { - 200} \right)}}{2}\\ = - 26\end{array}\)
b) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.\left( { - 0,5} \right)\)
\(\begin{array}{l} = \dfrac{2}{9} + \dfrac{1}{3}.\left( { - \dfrac{2}{3}} \right) + \dfrac{1}{2}.\left( {\dfrac{{ - 1}}{2}} \right)\\ = \dfrac{2}{9} + \dfrac{{ - 2}}{9} + \dfrac{{ - 1}}{4}\\ = \left( {\dfrac{2}{9} + \dfrac{{ - 2}}{9}} \right) + \dfrac{{ - 1}}{4}\\ = 0 + \dfrac{{ - 1}}{4}\\ = \dfrac{{ - 1}}{4}\end{array}\)
c) \(4.{\left( { - \dfrac{1}{2}} \right)^3} - 2.{\left( {\dfrac{{ - 1}}{2}} \right)^2} + 3.\left( { - \dfrac{1}{2}} \right) + 1\)
\(\begin{array}{l} = 4.\dfrac{{{{\left( { - 1} \right)}^3}}}{{{2^3}}} - 2.\dfrac{{{{\left( { - 1} \right)}^2}}}{{{2^2}}} + \dfrac{{ - 3}}{2} + 1\\ = 4.\dfrac{{ - 1}}{8} - 2.\dfrac{1}{4} + \dfrac{{ - 3}}{2} + 1\\ = \dfrac{{ - 1}}{2} - \dfrac{1}{2} + \dfrac{{ - 3}}{2} + \dfrac{2}{2}\\ = \dfrac{{ - 1 - 1 + \left( { - 3} \right) + 2}}{2}\\ = \dfrac{{ - 3}}{2}\end{array}\)
d) \(\dfrac{{{{\left( { - 0,7} \right)}^2}.{{\left( { - 5} \right)}^3}}}{{{{\left( {\dfrac{{ - 7}}{3}} \right)}^3}.{{\left( {\dfrac{3}{2}} \right)}^4}.{{\left( { - 1} \right)}^5}}}\)
\(\begin{array}{l} = \dfrac{{{{\left( {\dfrac{{ - 7}}{{10}}} \right)}^2}.{{\left( { - 5} \right)}^3}}}{{\dfrac{{{{\left( { - 7} \right)}^3}}}{{{3^3}}}.\dfrac{{{3^4}}}{{{2^4}}}.\left( { - 1} \right)}} = \dfrac{{\dfrac{{{{\left( { - 7} \right)}^2}}}{{{{\left( {2.5} \right)}^2}}}.{{\left( { - 1.5} \right)}^3}}}{{{{\left( { - 7} \right)}^3}.\dfrac{3}{{{2^4}}}.\left( { - 1} \right)}}\\ = \dfrac{{\dfrac{{{{\left( { - 7} \right)}^2}.{{\left( { - 1} \right)}^3}{{.5}^3}}}{{{2^2}{{.5}^2}}}}}{{\dfrac{{{{\left( { - 7} \right)}^3}.3.\left( { - 1} \right)}}{{{2^4}}}}} = \dfrac{{{{\left( { - 7} \right)}^2}.{{\left( { - 1} \right)}^3}{{.5}^3}}}{{{2^2}{{.5}^2}}}:\dfrac{{{{\left( { - 7} \right)}^3}.3.\left( { - 1} \right)}}{{{2^4}}}\\ = \dfrac{{{{\left( { - 7} \right)}^2}.{{\left( { - 1} \right)}^3}{{.5}^3}}}{{{2^2}{{.5}^2}}}.\dfrac{{{2^4}}}{{{{\left( { - 7} \right)}^3}.3.\left( { - 1} \right)}}\\ = \dfrac{1}{{\left( { - 7} \right)}}.\dfrac{{{{\left( { - 1} \right)}^2}}}{1}.\dfrac{5}{1}.\dfrac{{{2^2}}}{1}.\dfrac{1}{3}\\ = \dfrac{{5.4}}{{\left( { - 7} \right).3}} = \dfrac{{20}}{{ - 21}} = \dfrac{{ - 20}}{{21}}\end{array}\)
Bài 2:
Phương pháp:
Thực hiện phép tính, vận dụng quy tắc chuyển vế tìm \(x\)
Cách giải:
a) \({\left( {\dfrac{4}{5}} \right)^5}.x = {\left( {\dfrac{4}{5}} \right)^7}\)
\(\begin{array}{l}x = {\left( {\dfrac{4}{5}} \right)^7}:{\left( {\dfrac{4}{5}} \right)^5}\\x = {\left( {\dfrac{4}{5}} \right)^{7 - 5}} = {\left( {\dfrac{4}{5}} \right)^2}\\x = \dfrac{{{4^2}}}{{{5^2}}} = \dfrac{{16}}{{25}}\end{array}\)
Vậy \(x = \dfrac{{16}}{{25}}\)
b) \({\left( {0,03} \right)^3}:x = - {\left( {0,03} \right)^2}\)
\(\begin{array}{l}x = {\left( {0,03} \right)^3}:\left[ { - {{\left( {0,03} \right)}^2}} \right]\\x = - \left[ {{{\left( {0,03} \right)}^3}:{{\left( {0,03} \right)}^2}} \right]\\x = - {\left( {0,03} \right)^{3 - 2}}\\x = - 0,03\end{array}\)
Vậy \(x = - 0,03\)
c) \(\sqrt {0,16} + x = 3.\sqrt {0,09} .2\dfrac{1}{3}\)
\(\begin{array}{l}0,4 + x = 3.0,3.\dfrac{7}{3}\\0,4 + x = 0,3.7\\0,4 + x = 2,1\\x = 2,1 - 0,4\\x = 1,7\end{array}\)
Vậy \(x = 1,7\)
d) \(\sqrt {0,25} - 3x - \sqrt {0,49} .\dfrac{1}{7} = \sqrt {0,04} .\dfrac{1}{2}\)
\(\begin{array}{l}0,5 - 3x - 0,7.\dfrac{1}{7} = 0,2.\dfrac{1}{2}\\0,5 - 3x - 0,1 = 0,1\\0,4 - 3x = 0,1\\3x = 0,4 - 0,1\\3x = 0,3\\x = 0,3:3\\x = 0,1\end{array}\)
Vậy \(x = 0,1\)
Bài 3:
Phương pháp:
Vận dụng tính chất tia phân giác của một góc
Dấu hiệu nhận biết hai góc kề bù
Cách giải:
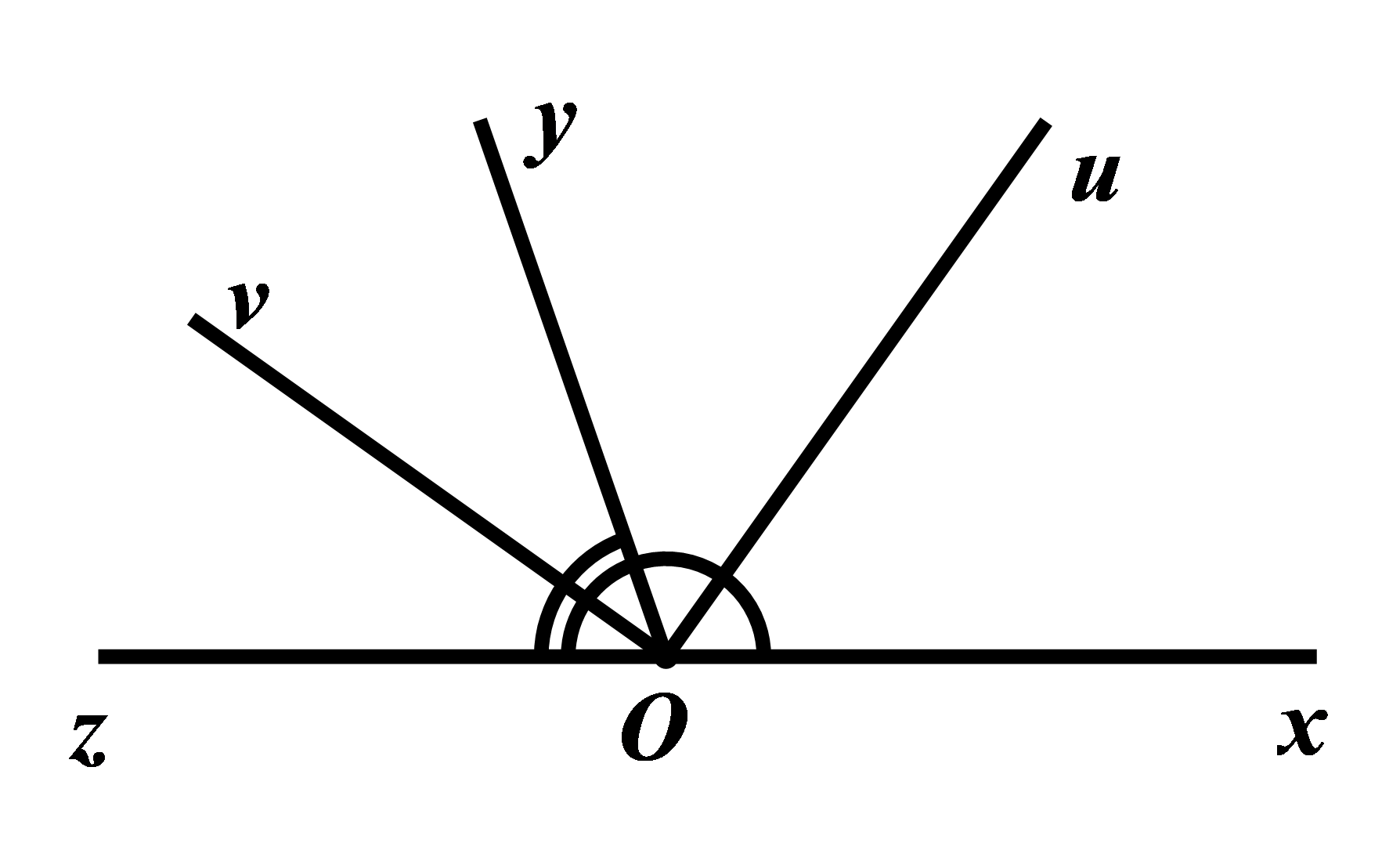
Vì \(Ou\) là tia phân giác của \(\angle xOy\) nên \(\angle xOy = 2\angle uOy\) (tính chất tia phân giác của một góc)
\(Ov\) là tia phân giác của \(\angle yOz\) nên \(\angle yOz = 2\angle yOv\) (tính chất tia phân giác của một góc)
Ta có: \(\angle xOy + \angle yOz = 2\angle uOy + 2\angle yOv\)
\(\begin{array}{l} = 2.\left( {\angle uOy + \angle yOv} \right)\\ = 2.\angle uOv\\ = {2.90^0} = {180^0}\end{array}\)
Do đó, hai góc \(xOy\) và \(yOz\) là hai góc kề bù.
Bài 4:
Phương pháp:
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau.
- Dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt đường thẳng phân biệt a và b, và trong các góc tạo thành có một cặp góc so le trong bằng nhau hoặc một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
Cách giải:
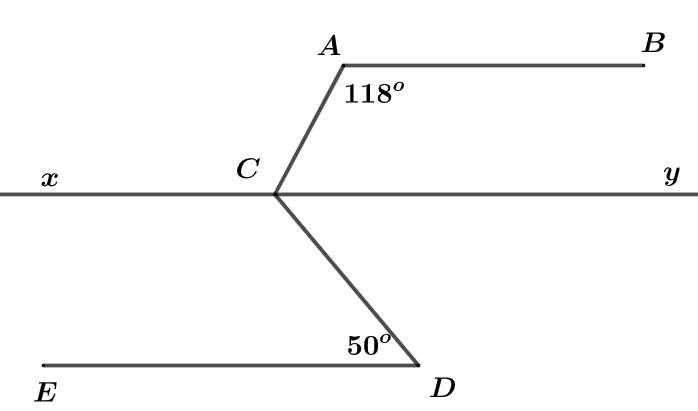
Qua \(C\) kẻ đường thẳng \(xy\) sao cho \(xy\,//\,AB\)
Vì \(xy\,//\,AB\) (cách dựng) \( \Rightarrow \angle BAC = \angle ACx\) (hai góc so le trong)
\( \Rightarrow \angle ACx = {118^o}\)
Ta có \(\angle ACx + \angle ACy = {180^o}\) (2 góc kề bù) \( \Rightarrow \angle ACy = {180^o} - \angle ACx = {180^o} - {118^o} = {62^o}\)
Ta lại có \(\left\{ \begin{array}{l}xy\,//\,AB\,\left( {cd} \right)\\AB\,//\,ED\,\left( {gt} \right)\end{array} \right. \Rightarrow xy\,//\,ED \Rightarrow \angle EDC = \angle DCy\) (so le trong)
\( \Rightarrow \angle DCy = {50^o}\)
Mà \(\angle ACD = \angle ACy + \angle DCy = {62^o} + {50^o} = {112^o}.\)
Bài 5:
Phương pháp:
Đánh giá biểu thức \(A \ge k\left( {k \in \mathbb{R}} \right) \Rightarrow \min A = k\)
Chú ý: Bình phương 1 số luôn lớn hơn hoặc bằng 0
Cách giải:
Ta có: \({\left( {2x + 1} \right)^2} \ge 0\) với mọi số thực \(x\) nên \(\dfrac{{2{{\left( {2x + 1} \right)}^2}}}{5} \ge 0,\forall x \in \mathbb{R}\)
\(A = \dfrac{{2{{\left( {2x + 1} \right)}^2}}}{5} - {2023^0} = \dfrac{{2{{\left( {2x + 1} \right)}^2}}}{5} - 1 \ge - 1,\forall x \in \mathbb{R}\)
Dấu “=” xảy ra \( \Leftrightarrow 2x + 1 = 0 \Leftrightarrow x = \dfrac{{ - 1}}{2}\)
Vậy \(\min A = - 1\) khi \(x = \dfrac{{ - 1}}{2}\)
Phương pháp giải:
- Đề thi giữa kì 1 Toán 7 - Đề số 6 - Kết nối tri thức
- Đề thi giữa kì 1 Toán 7 - Đề số 7 - Kết nối tri thức
- Đề thi giữa kì 1 Toán 7 - Đề số 8 - Kết nối tri thức
- Đề thi giữa kì 1 Toán 7 - Đề số 9 - Kết nối tri thức
- Đề thi giữa kì 1 Toán 7 - Đề số 10 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay












Danh sách bình luận