Phương pháp giải:

- Tính \(y'\).

- Hàm số đồng biến trên \(\left[ {2; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left[ {2; + \infty } \right)\).

- Giải bất phương trình \(a{x^2} + bx + c > 0\,\,\forall x \in \left( {\alpha ;\beta } \right)\).

   + TH1: \(\left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\).

   + TH2: \(\Delta  > 0\), phương trình có 2 nghiệm phân biệt \({x_1} < {x_2}\). Tìm điều kiện để \(\left( {\alpha ;\beta } \right)\) là tập con của tập nghiệm của bất phương trình  \(a{x^2} + bx + c > 0\).

Lời giải chi tiết:

Hàm số đã cho xác định trên \(\left[ {2; + \infty } \right)\).

Ta có: \(y' = 3{x^2} - 2mx - 2{m^2} + 7m - 7\).

Để hàm số đồng biến trên \(\left[ {2; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left[ {2; + \infty } \right)\)

\( \Leftrightarrow 3{x^2} - 2mx - 2{m^2} + 7m - 7 \ge 0\,\,\forall x \in \left[ {2; + \infty } \right)\,\,\left( 1 \right)\).

Ta có:

\(\begin{array}{l}\Delta ' = {m^2} - 3\left( { - 2{m^2} + 7m - 7} \right)\\\Delta ' = 7{m^2} - 21m + 21 > 0\,\,\forall m \in \mathbb{R}\end{array}\)

Khi đó \(y' = 0\) có 2 nghiệm \({x_1},\,\,{x_2}\) phân biệt (giả sử \({x_1} < {x_2}\)).

Khi đó bất phương trình (1) có sơ đồ miền nghiệm là:

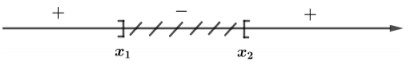
Ta có \(y' \ge 0\,\,\forall x \in \left[ {2; + \infty } \right)\) \( \Leftrightarrow \left[ {2; + \infty } \right) \subset S\).

\(\begin{array}{l} \Leftrightarrow {x_1} < {x_2} \le 2\\ \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} < 4\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} < 4\\{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4 \ge 0\end{array} \right.\,\,\left( * \right)\end{array}\)

Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{2m}}{3}\\{x_1}{x_2} = \dfrac{{ - 2{m^2} + 7m - 7}}{3}\end{array} \right.\).

\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2m}}{3} < 4\\\dfrac{{ - 2{m^2} + 7m - 7}}{3} - 2.\dfrac{{2m}}{3} + 4 \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < 6\\ - 2{m^2} + 7m - 7 - 4m + 12 \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < 6\\ - 2{m^2} + 3m + 5 \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < 6\\ - 1 \le m \le \dfrac{5}{2}\end{array} \right. \Leftrightarrow  - 1 \le m \le \dfrac{5}{2}\end{array}\)   

Vậy \(m \in \left[ { - 1;\dfrac{5}{2}} \right]\).

Chọn A.