Câu hỏi
Xác định giá trị của tham số \(m\) để hàm số \(y = {x^3} - 3m{x^2} - m\) nghịch biến trên khoảng \(\left( {0;1} \right)\).
- A \(m \ge \dfrac{1}{2}\)
- B \(m < \dfrac{1}{2}\)
- C \(m \le 0\)
- D \(m \ge 0\)
Phương pháp giải:
- Bước 1: Nêu điều kiện để hàm số đơn điệu trên D:
+ Hàm số \(y = f\left( x \right)\) nghịch biến trên \(D \Leftrightarrow y' = f'\left( x \right) \le 0\) với mọi \(x \in D\).
- Bước 2: Từ điều kiện trên sử dụng các cách suy luận khác nhau cho từng bài toán để tìm \(m\).
+ Biện luận theo \(m\) để xét dấu đạo hàm.
- Bước 3: Kết luận.
Lời giải chi tiết:
Ta có: \(y' = 3{{\rm{x}}^2} - 6m{\rm{x}}\) \( \Rightarrow y' = 0 \Leftrightarrow x = 0\) hoặc \(x = 2m\).
Trường hợp 1: \(m < 0\)
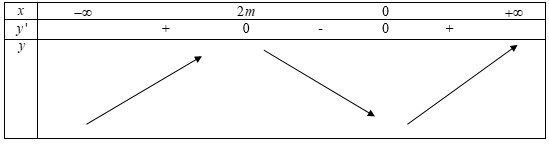
Dễ thấy hàm số trên khoảng \(\left( {0;1} \right)\) đồng biến với mọi \(m < 0\) (loại)
Trường hợp 2: \(m = 0\)
Với \(m=0\) thì \(y'=3x^2 \ge 0\) nên hàm số đồng biến trên \(R\).
Do đó hàm số đồng biến trên \(\left( {0;1} \right)\) (loại)
Trường hợp 3: \(m > 0\)
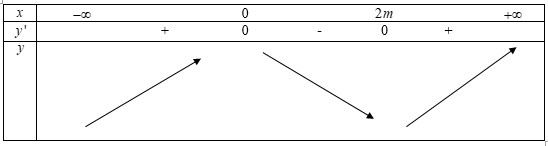
Dễ thấy hàm số trên khoảng \(\left( {0;1} \right)\) nghịch biến \( \Leftrightarrow 2m \ge 1 \Leftrightarrow m \ge \dfrac{1}{2}\).
Chọn A.







