Câu hỏi
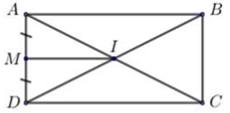
Trong mặt phẳng với hệ tọa độ \(Oxy,\) cho hình chữ nhật \(ABCD\) có diện tích bằng 10, tâm \(I\left( {1;1} \right)\)biết trung điểm \(AD\) là \(M\left( {0; - 1} \right).\) Với \({x_D} < 0\), tọa độ điểm \(D\) là
- A \(\left( { - 1;\frac{1}{2}} \right)\)
- B \(\left( { - 1;\frac{{ - 1}}{2}} \right)\)
- C \(\left( { - 1;\frac{{ - 3}}{2}} \right)\)
- D \(\left( { - 1;\frac{3}{2}} \right)\)
Phương pháp giải:
Viết phương trình đường thẳng \(AD\) rồi tham số hóa điểm \(D\). Tính \(AD\) được từ diện tích \(ABCD\)
Lời giải chi tiết:
\(\overrightarrow {IM} = \left( { - 1; - 2} \right) \Rightarrow IM = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \Rightarrow AB = 2IM = 2\sqrt 5 \)
\(S = 10 \Rightarrow AB.AD = 10 \Leftrightarrow 2\sqrt 5 .AD = 10 \Rightarrow AD = \sqrt 5 \)
\(AD:\left\{ \begin{array}{l}qua\,M\left( {0; - 1} \right)\\ \bot \overrightarrow {IM} = \left( { - 1; - 2} \right) \Rightarrow \overrightarrow {{n_{AD}}} = \left( {1;2} \right)\end{array} \right. \Rightarrow AD:\,x + 2y + 2 = 0\)
\( \Rightarrow D\left( { - 2t - 2;t} \right) \Rightarrow A = 2M - D = \left( {2t + 2; - 2 - t} \right)\)
\(\begin{array}{l}\overrightarrow {DA} = \left( {4t + 4; - 2 - 2t} \right) \Rightarrow D{A^2} = {\left( {4t + 4} \right)^2} + {\left( { - 2 - 2t} \right)^2} = 5\\ \Leftrightarrow 20{t^2} + 40t + 15 = 0 \Rightarrow \left[ \begin{array}{l}t = \frac{{ - 1}}{2} \Rightarrow D\left( { - 1;\frac{{ - 1}}{2}} \right)\\t = \frac{{ - 3}}{2} \Rightarrow D\left( {1;\frac{{ - 3}}{2}} \right)\end{array} \right.\end{array}\)
Chọn B.