Câu hỏi
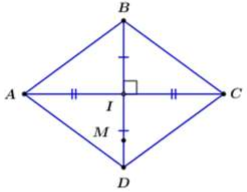
Trong mặt phẳng với hệ tọa độ \(Oxy,\) cho hình thoi \(ABCD\) có phương trình đường thẳng \(AB:3x - y + 2 = 0;\,\,AD:x - 3y + 4 = 0\). Điểm \(M\left( {1;1} \right)\) thuộc đường thẳng \(BD\). Tọa độ điểm \(B\) là
- A \(B\left( {1; - 1} \right)\)
- B \(B\left( {2;0} \right)\)
- C \(B\left( { - 1;1} \right)\)
- D \(B\left( {0;2} \right)\)
Phương pháp giải:
Tìm \(B\) bằng cách tìm giao của 2 đường thẳng \(AB,\,\,BD\). Muốn vậy phải viết phương trình đường thẳng \(BD\) dựa vào phân giác \(AC\) của \(\angle BAD\)
Lời giải chi tiết:
Phân giác \(AC\) của \(\angle BAD\) có pt \(\frac{{3x - y + 2}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = \pm \frac{{x - 3y + 4}}{{\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }}\)
\( \Rightarrow \left[ \begin{array}{l}3x - y + 2 = x - 3y + 4\\3x - y + 2 = - x + 3y - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x + 2y - 2 = 0\\4x - 4y + 6 = 0\end{array} \right.\)
+ TH1: Nếu phương trình \(AC:2x + 2y - 2 = 0\)
Vì \( \Rightarrow BD\left\{ \begin{array}{l}qua\,M\left( {1;1} \right)\\ \bot AC \Rightarrow \overrightarrow {{n_{BD}}} = \left( {1; - 1} \right)\end{array} \right. \Rightarrow BD:x - y = 0\)
\( \Rightarrow B = BD \cap AB = \left( { - 1; - 1} \right)\)
+ TH2: Nếu phương trình \(AC:4x - 4y + 6 = 0\)
Vì \( \Rightarrow BD\left\{ \begin{array}{l}qua\,M\left( {1;1} \right)\\ \bot AC \Rightarrow \overrightarrow {{n_{BD}}} = \left( {1;1} \right)\end{array} \right. \Rightarrow BD:x + y - 2 = 0\)
\( \Rightarrow B = BD \cap AB = \left( {0;2} \right)\)
Chọn D.