Câu hỏi
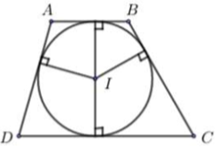
Trong mặt phẳng với hệ tọa độ \(Oxy,\) cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {y^2} = 2\) nội tiếp hình thang \(ABCD\) \(\left( {AB//CD} \right)\) với \(A\left( {1;2} \right);\,\,B\left( {3;0} \right)\)ba điểm \(A\left( {2;\,0} \right),\,\,B\left( {0;\,3} \right).\) Tọa độ đỉnh \(D\) là
- A \(D\left( {1;0} \right)\)
- B \(D\left( { - 1;0} \right)\)
- C \(D\left( {2;1} \right)\)
- D \(D\left( {2; - 1} \right)\)
Phương pháp giải:
Tìm \(D\) bằng cách tìm giao giữa hai đường thẳng \(AD,\,\,CD\). Để viết phương trình đường thẳng \(AD,\,\,CD\) thì ta cần phải sử dụng công thức khoảng cách từ tâm đường tròn nội tiếp đến các cạnh bằng bán kính
Lời giải chi tiết:
\(\left( C \right)\) có tâm \(I\left( {1;0} \right),\,\,R = \sqrt 2 \)
\(\overrightarrow {AB} = \left( {2; - 2} \right) \Rightarrow \overrightarrow {{n_{AB}}} = \left( {1;1} \right) \Rightarrow AB:x + y - 3 = 0\)
Do \(AB//CD \Rightarrow CD:\,\,x + y + c = 0\,\,\,\left( {c \ne - 3} \right)\)
\(CD\) tiếp xúc với \(\left( C \right) \Rightarrow d\left( {I;CD} \right) = R \Rightarrow \frac{{\left| {0 + 1 + c} \right|}}{{\sqrt 2 }} = \sqrt 2 \)
\(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}1 + c = 2\\1 + c = - 2\end{array} \right. \Rightarrow \left[ \begin{array}{l}c = 1\,\,\,\,\,\,\left( {tm} \right)\\c = - 3\,\,\,\left( {ktm} \right)\end{array} \right.\\ \Rightarrow CD:x + y + 1 = 0\end{array}\)
Giả sử phương trình \(AD\) có dạng \(y - 2 = k\left( {x - 1} \right) \Leftrightarrow kx - y + 2 - k = 0\)
\(\begin{array}{l}d\left( {I,AD} \right) = R \Leftrightarrow \frac{{\left| {k - 0 + 2 - k} \right|}}{{\sqrt {{k^2} + 1} }} = \sqrt 2 \Leftrightarrow \frac{{\left| 2 \right|}}{{\sqrt {{k^2} + 1} }} = \sqrt 2 \Rightarrow 2 = \sqrt {2.\left( {{k^2} + 1} \right)} \\ \Leftrightarrow 4 = 2\left( {{k^2} + 1} \right) \Leftrightarrow 2{k^2} = 2 \Rightarrow \left[ \begin{array}{l}k = 1 \Rightarrow x - y + 1 = 0\\k = - 1 \Rightarrow - x - y + 3 = 0 \Rightarrow x + y - 3 = 0\left( {ktm\,\,do\, \equiv AB} \right)\end{array} \right.\\ \Rightarrow AD:x - y + 1 = 0\end{array}\)
\(D = AD \cap CD \Rightarrow D\left\{ \begin{array}{l}x + y + 1 = 0\\x - y + 1 = 0\end{array} \right. \Rightarrow D\left( { - 1;0} \right)\)
Chọn B.