Câu hỏi
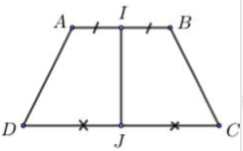
Trong mặt phẳng \(\left( {Oxy} \right)\) cho hình thang cân \(ABCD\,\,\left( {AB//CD} \right),A\left( {8;4} \right);\,B\left( { - 2;6} \right);\,C\left( {5;0} \right)\). Tọa độ đỉnh \(D\) là
- A \(D\left( {\frac{2}{{13}};\frac{3}{{13}}} \right)\)
- B \(D\left( {\frac{{ - 1}}{{13}};\frac{5}{{13}}} \right)\)
- C \(D\left( {\frac{{55}}{{26}};\frac{{15}}{{26}}} \right)\)
- D \(D\left( {\frac{{ - 10}}{{13}};\frac{{15}}{{13}}} \right)\)
Phương pháp giải:
Phương trình đường thẳng đi qua điểm \(M\left( {{x_0};\,{y_0}} \right)\) và có hệ số góc \(k\) có phương trình: \(y = k\left( {x - {x_0}} \right) + {y_0}.\)
Lời giải chi tiết:
\(CD:\left\{ \begin{array}{l}qua\,\,C\left( {5;0} \right)\\//AB \Rightarrow \overrightarrow {{u_{CD}}} = \overrightarrow {AB} = \left( { - 10;2} \right) \Rightarrow \overrightarrow {{n_{CD}}} = \left( {1;5} \right)\end{array} \right. \Rightarrow CD:x + 5y - 5 = 0\)
Gọi \(I,\,J\) lần lượt là trung điểm của hai đường thẳng \(AB,\,CD \Rightarrow IJ \bot AB;\,IJ \bot CD\) (tính chất hình thang cân)
\( \Rightarrow I = \frac{{A + B}}{2} \Rightarrow I\left( {3;5} \right)\)
Đường thẳng \(IJ\left\{ \begin{array}{l}qua\,\,I\left( {3;5} \right)\\ \bot AB \Rightarrow \overrightarrow {{n_{IJ}}} = \overrightarrow {AB} = \left( { - 10;2} \right)//\left( { - 5;1} \right)\end{array} \right. \Rightarrow IJ: - 5x + y + 10 = 0\)
Ta có \(J = IJ \cap CD \Rightarrow \left\{ \begin{array}{l} - 5x + y + 10 = 0\\x + 5y - 5 = 0\end{array} \right. \Rightarrow J\left( {\frac{{55}}{{26}};\frac{{15}}{{26}}} \right)\)
Do \(J\) là trung điểm \(CD \Rightarrow J = \frac{{C + D}}{2} \Rightarrow D = 2J - C \Rightarrow D\left( {\frac{{ - 10}}{{13}};\frac{{15}}{{13}}} \right)\)
Chọn D.