Phương pháp giải:

Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.

Lời giải chi tiết:

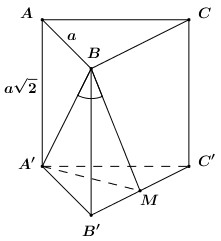
Gọi \(M\) là trung điểm của \(B'C'\), do \(\Delta A'B'C'\) đều nên \(A'M \bot B'C'\).

Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\,\,\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right. \Rightarrow A'M \bot \left( {BCC'B'} \right)\).

\( \Rightarrow MB\) là hình chiếu của \(A'B\) trên \(\left( {BCC'B'} \right)\).

\( \Rightarrow \angle \left( {A'B;\left( {BCC'B'} \right)} \right) = \angle \left( {A'B;MB} \right) = \angle A'BM\).

Do \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM \Rightarrow \Delta A'BM\) vuông tại \(M\).

Tam giác \(A'B'C'\) đều cạnh \(a \Rightarrow A'M = \dfrac{{a\sqrt 3 }}{2}\).

\(\Delta A'AB\) vuông tại \(A\) (do \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot AB\)) nên áp dụng định lí Pytago ta có: \(A'B = \sqrt {AA{'^2} + A{B^2}}  = \sqrt {2{a^2} + {a^2}}  = a\sqrt 3 \).

Xét tam giác vuông \(A'BM\) có: \(\sin \angle A'BM = \dfrac{{A'M}}{{A'B}} = \dfrac{{\dfrac{{a\sqrt 3 }}{2}}}{{a\sqrt 3 }} = \dfrac{1}{2} \Rightarrow \angle A'BM = {30^0}\).

Vậy \(\angle \left( {A'B;\left( {BCC'B'} \right)} \right) = {30^0}\).

Chọn B.