Giải SBT toán hình học và đại số 11 nâng cao Ôn tập chương III. Vectơ trong không gian. Quan hệ vuôn..

Câu 77 trang 129 Sách bài tập Hình học 11 Nâng cao


Giải bài tập Câu 77 trang 129 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình chóp S.ABC có đáy là tam giác đều, SA = SB = SC = a và cùng tạo với mặt phẳng (ABC) góc 60°. Một mặt phẳng song song với hai cạnh chéo nhau của hình chóp và cắt hình chóp đó theo thiết diện là hình vuông. Tính diện tích thiết diện.

Lời giải chi tiết

 

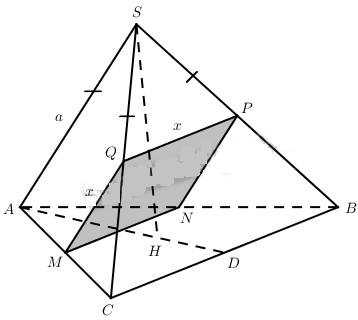
Giả sử H là tâm của tam giác đều.

Từ SA = SB = SC nên \(SH \bot \left( {ABC} \right)\) và \(\widehat {SAH} = {60^0}\).

Giả sử mặt phẳng song song với SA, CD và thiết diện thu được là hình vuông MNPQ.

Khi đó, nếu kí hiệu cạnh hình vuông là x thì:

\(\eqalign{  & {x \over {SA}} = {{CQ} \over {C{\rm{S}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)  \cr  & {x \over {BC}} = {{SQ} \over {SC}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right) \cr} \)

Từ (1), (2) suy ra:

\(\eqalign{  & x\left( {{1 \over {SA}} + {1 \over {BC}}} \right) = {{CQ + Q{\rm{S}}} \over {C{\rm{S}}}} = 1  \cr  &  \Rightarrow x= {{SA.BC} \over {SA + BC}} = {{a.BC} \over {a + BC}} \cr} \)

Mặt khác \(HA = SA\cos {60^0} = {a \over 2}\).

mà \(HA = {{BC\sqrt 3 } \over 3}\).

Suy ra \(BC = {{a\sqrt 3 } \over 2}\).

Từ đó \(x = {{a.{{a\sqrt 3 } \over 2}} \over {a + {{a\sqrt 3 } \over 2}}} = {{a\sqrt 3 } \over {2 + \sqrt 3 }} = a\sqrt 3 \left( {2 - \sqrt 3 } \right)\).

Vậy \({S_{MNPQ}} = {\left[ {a\sqrt 3 \left( {2 - \sqrt 3 } \right)} \right]^2} = 3{{\rm{a}}^2}{\left( {2 - \sqrt 3 } \right)^2}\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store