Cách vẽ phép quay bằng phần mềm GeoGebra - Toán 9
1. Phép quay
Phép quay là một phép biến đổi hình học quay một hình quanh một điểm cố định, gọi là tâm quay, một góc xác định.
2. Phép quay thuận chiều
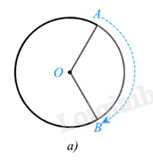
Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a).
3. Phép quay ngược chiều
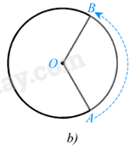
Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b).
Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
4. Phép quay giữ nguyên một đa giác
Cho hình đa giác đều \({A_1}{A_2} \ldots {A_n}(n \ge 3,n \in {\rm{N}})\) có tâm \(O\). Phép quay giữ nguyên hình đa giác đều \({A_1}{A_2} \ldots {A_n}\) là phép quay tâm \(O\) biến mỗi đỉnh của hình đa giác đều thành một đỉnh của hình đa giác đểu đó.
5. Cách vẽ phép quay bằng phần mềm GeoGebra
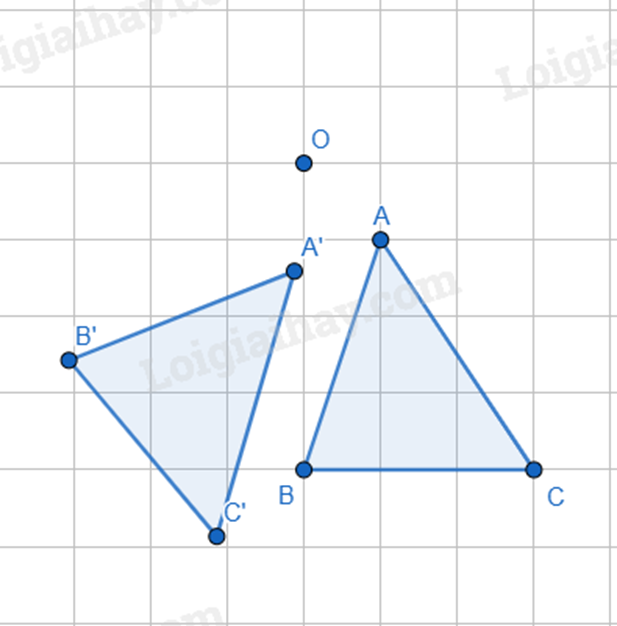
Ta có thể vẽ tam giác A’B’C’ có được qua phép quay thuận chiều \(50^\circ \) tâm O tam giác ABC như sau:
- Dùng  để vẽ tam giác ABC.
để vẽ tam giác ABC.
- Dùng  và đổi tên điểm (nếu cần) để vẽ điểm O.
và đổi tên điểm (nếu cần) để vẽ điểm O.
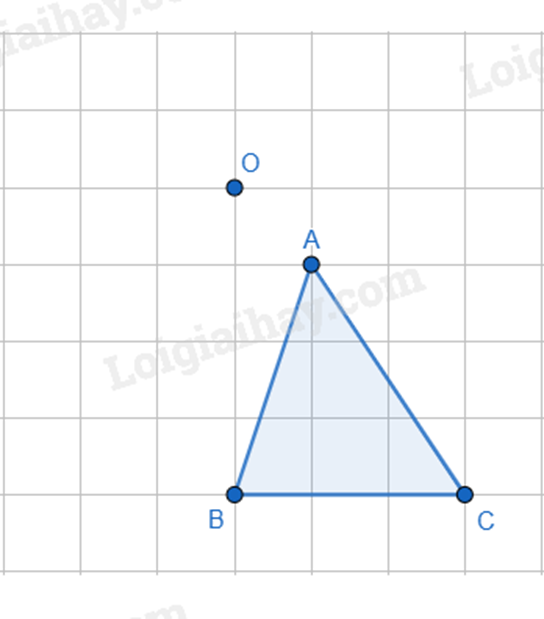
- Dùng  (nháy chuột vào tam giác ABC, điểm O, nhập vào \(50^\circ \) và lựa chọn theo chiều kim đồng hồ) để vẽ tam giác A’B’C’.
(nháy chuột vào tam giác ABC, điểm O, nhập vào \(50^\circ \) và lựa chọn theo chiều kim đồng hồ) để vẽ tam giác A’B’C’.
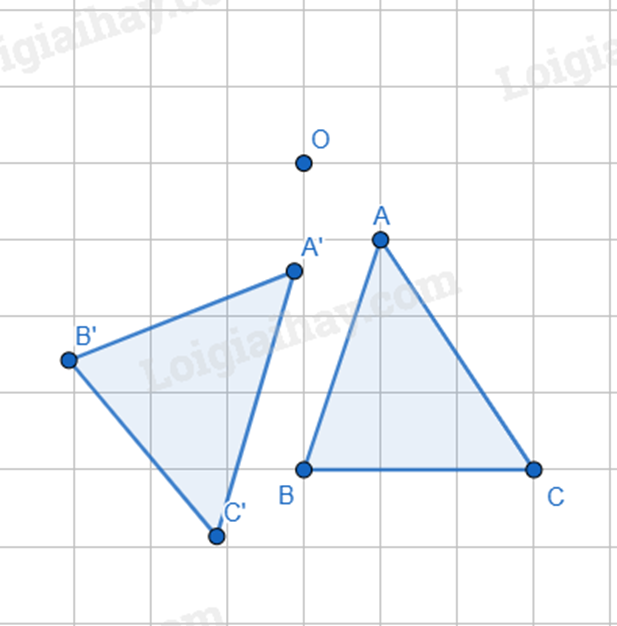
Trong hình vẽ dưới đây, tam giác A’B’C’ có được qua phép quay thuận chiều \(50^\circ \) tâm O tam giác ABC: