Copyright © 2021 loigiaihay.com
Từ điển Toán 12 | Các dạng bài tập Toán 12
Vecto trong không gian - Toán 12
Vecto trong không gian - Toán 12 Các khái niệm liên quan đến vecto trong không gian - Toán 12
1. Khái niệm vecto
Vecto trong không gian là một đoạn thẳng có hướng.
2. Độ dài vecto
Độ dài của vecto trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vecto đó.
+ \(\overrightarrow {AB} \) có điểm đầu là A, điểm cuối là B.
+ Độ dài của \(\overrightarrow {AB} \) là \(\left| {\overrightarrow {AB} } \right|\).
+ Các vecto có điểm đầu và điểm cuối trùng nhau gọi là vecto-không.
3. Hai vecto cùng phương, cùng hướng
Hai vecto được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
Nếu hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.
Vecto-không cùng hướng với mọi vecto.
4. Hai vecto bằng nhau
Hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.
5. Ví dụ minh hoạ về các khái niệm liên quan đến vecto
Cho hình lập phương ABCD.A’B’C’D’:
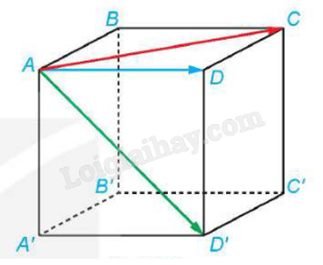
Một số vecto có điểm đầu là A: \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AC'} ,\overrightarrow {AA'} ,...\)
Một số vecto có độ dài bằng nhau: \(\left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {AA'} } \right| = \left| {\overrightarrow {C'D'} } \right| = ...\)
Một số vecto cùng phương: \(\overrightarrow {AB} ,\overrightarrow {CD} ,\overrightarrow {C'D'} ,...\)
Một số vecto cùng hướng: \(\overrightarrow {AD'} ,\overrightarrow {BC'} \).
