SBT Tin 11, giải sbt tin học 11 kết nối tri thức Chủ đề 6. Kĩ thuật lập trình SBT Tin học 11 Kết nối tri..

Bài 24. Đánh giá độ phức tạp thời gian thuật toán trang 75 SBT Tin học 11 Kết nối tri thức với cuộc sống


Giả sử một chương trình P mô tả một thuật toán nào đó. Người ta đo được các thông tin thời gian sau:

Lựa chọn câu để xem lời giải nhanh hơn

24.1

Giả sử một chương trình P mô tả một thuật toán nào đó. Người ta đo được các thông tin thời gian sau:

T1 = thời gian chương trình nhập dữ liệu input và đưa vào bộ nhớ.

T2 = thời gian chạy chương trình từ khi nhập xong dữ liệu input và tính xong dữ liệu output.

T3 = thời gian đưa dữ liệu output ra thiết bị ngoài chuẩn.

Khi đó thời gian chạy chương trình T(n) dùng để tính độ phức tạp thời gian của thuật toán là phương án nào trong các phương án sau?

A. T1 + T2.

B. T2.

C. T2+T3.

Lời giải chi tiết:

Đáp án đúng là: B. T2. T2 = thời gian chạy chương trình từ khi nhập xong dữ liệu input và tính xong dữ liệu output

Quảng cáo

Lộ trình SUN 2026

24.2

Đánh giá thời gian chạy của chương trình sau:

Đánh giá thời gian chạy của chương trình sau

Lời giải chi tiết:

Đánh giá thời gian chạy của chương trình như sau: T(n) = n+2

24.3

Đánh giá thời gian chạy của chương trình sau:

Đánh giá thời gian chạy của chương trình sau

Lời giải chi tiết:

Đánh giá thời gian chạy của chương trình sau: T(n) = 2log2n + 2

24.4

Đánh giá thời gian chạy của chương trình sau, trong đó A là ma trận vuông bậc n.

Đánh giá thời gian chạy của chương trình sau, trong đó A là ma trận vuông bậc n

Lời giải chi tiết:

Đánh giá thời gian chạy của chương trình sau, trong đó A là ma trận vuông bậc n.

T(n) = n2 + 2.

24.5

Đánh giá thời gian chạy của chương trình sau tính theo đơn vị thời gian, A là một dãy số cho trước có n phần tử.

Đánh giá thời gian chạy của chương trình sau tính theo đơn vị thời gian

Lời giải chi tiết:

T(n) = (3/2).n2 + (5/2)n + 1 trong trường hợp xấu nhất.

24.6

Đánh giá thời gian chạy của thuật toán sắp xếp chèn đã học trong sách giáo khoa.

Lời giải chi tiết:

T(n) = 2n2 – 3n + 2 trong trường hợp xấu nhất.

24.7

Đánh giá thời gian chạy của thuật toán sắp xếp nổi bọt đã học trong sách giáo khoa

Lời giải chi tiết:

T(n) = 2n2 – 2n + 1 trong trường hợp xấu nhất.

24.8

Tính độ phức tạp của các hàm sau theo kí hiệu O-lớn

a) n + 2n.log(n) + 10.

b) 2n2 + 3n3log(n) + n3/2.

c) 2" + 3" + 5".

Lời giải chi tiết:

a) O(nlogn);

b) O(n3.logn);

c) O(5")

24.9

a) Chứng minh n = O(n2).

b) Chứng minh n2 = O(n)

Lời giải chi tiết:

a) Vì hiển nhiên n < n với n > 1 nên suy ra n = O(n).

b) Nếu như n2 = O(n) thì ta phải có n2 < C.n với n đủ lớn, nhưng từ bất đẳng thức này suy ra n < C. Mâu thuẫn. Vậy suy ra n = O(n).

24.10

Chứng minh rằng nếu f(n) = O(g(n)) và g(n) = O(h(n)) thì ta có: f(n) = O(h(n)).

Lời giải chi tiết:

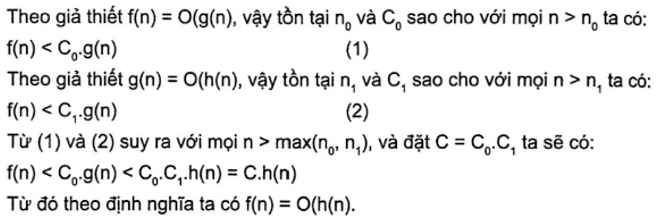
Chứng minh rằng nếu f(n) = O(g(n)) và g(n) = O(h(n)) thì ta có: f(n) = O(h(n)).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store