-
Giải Toán 12 tập 1 - Cùng khám phá
-
Giải Toán 12 tập 2 - Cùng khám phá
-
Nội dung đang cập nhật
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Bài 1. Tính đơn điệu và cực trị của hàm số - Toán 12 Cù..
Lý thuyết Tính đơn điệu và cực trị của hàm số Toán 12 Cùng khám phá
1. Tính đơn điệu của hàm số và dấu của đạo hàm Định lý
1. Tính đơn điệu của hàm số và dấu của đạo hàm
Định lý
|
Cho hàm số y = f(x) có đạo hàm trên khoảng (a;b), (có thể a là \( - \infty \);b là \( + \infty \)). - Hàm số y = f(x) đồng biến trên khoảng K nếu f’(x) > 0. - Hàm số y = f(x) đồng biến trên khoảng K nếu f’(x) < 0. |
Ví dụ: Hàm số \(y = {x^2} - 4x + 2\) có y’ = 2x – 4.
- y’ > 0 với \(x \in (2; + \infty )\) nên HS đồng biến trên khoảng \(\left( {2; + \infty } \right)\).
- y’ < 0 với \(x \in ( - \infty ;2)\) nên HS đồng biến trên khoảng \(\left( { - \infty ;2} \right)\).
Định lý mở rộng
|
Cho hàm số y = f(x) có đạo hàm trên khoảng (a;b). - Nếu f’(x) 0 với mọi x thuộc (a;b) và f’(x) = 0 chỉ tại một số hữa hạn điểm thuộc khoảng (a;b) thì hàm số f(x) đồng biến trên khoảng (a;b). - Nếu f’(x) 0 với mọi x thuộc (a;b) và f’(x) = 0 chỉ tại một số hữa hạn điểm thuộc khoảng (a;b) thì hàm số f(x) nghịch biến trên khoảng (a;b). |
2. Cực trị của hàm số
Khái niệm cực trị của hàm số
|
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\). - Nếu tồn tại số h > 0 sao cho f(x) < f(\({x_0}\)) \(\forall x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì hàm số f(x) đạt cực đại tại \({x_0}\). - Nếu tồn tại số h > 0 sao cho f(x) > f(\({x_0}\)) \(\forall x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì hàm số f(x) đạt cực tiểu tại \({x_0}\). |
Ví dụ: Cho đồ thị của hàm số y = f(x) như sau:
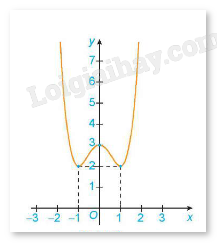
Hàm số đạt cực tiểu tại x = -1 và \({y_{CT}}\)= y(-1) = 2.
Hàm số đạt cực đại tại x = 0 và = y(0) = 3.
Hàm số đạt cực tiểu tại x = 1 và \({y_{CT}}\)= y(1) = 2.
Định lí (điều kiện đủ để hàm số có cực trị)
|
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó: - Nếu f’(x) < 0 \(\forall x \in \left( {a;{x_0}} \right)\) và f’(x) > 0 \(\forall x \in \left( {{x_0};b} \right)\) thì \({x_0}\) là một điểm cực tiểu của hàm số f(x). - Nếu f’(x) > 0 \(\forall x \in \left( {a;{x_0}} \right)\) và f’(x) < 0 \(\forall x \in \left( {{x_0};b} \right)\) thì \({x_0}\) là một điểm cực đại của hàm số f(x). |
Ví dụ: Tìm cực trị của hàm số \(y = {x^3} - 6{x^2} + 9x + 30\).
Tập xác định của hàm số là R.
Ta có: \(y' = 3{x^2} - 12x + 9\); y’ = 0 \( \Leftrightarrow \)x = 1 hoặc x = 3.
BBT:
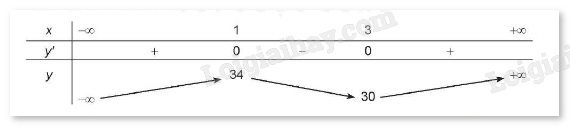
Hàm số đạt cực đại tại x = 1 và = y(1) = 34.
Hàm số đạt cực tiểu tại x = 3 và \({y_{CT}}\)= y(3) = 30.
|
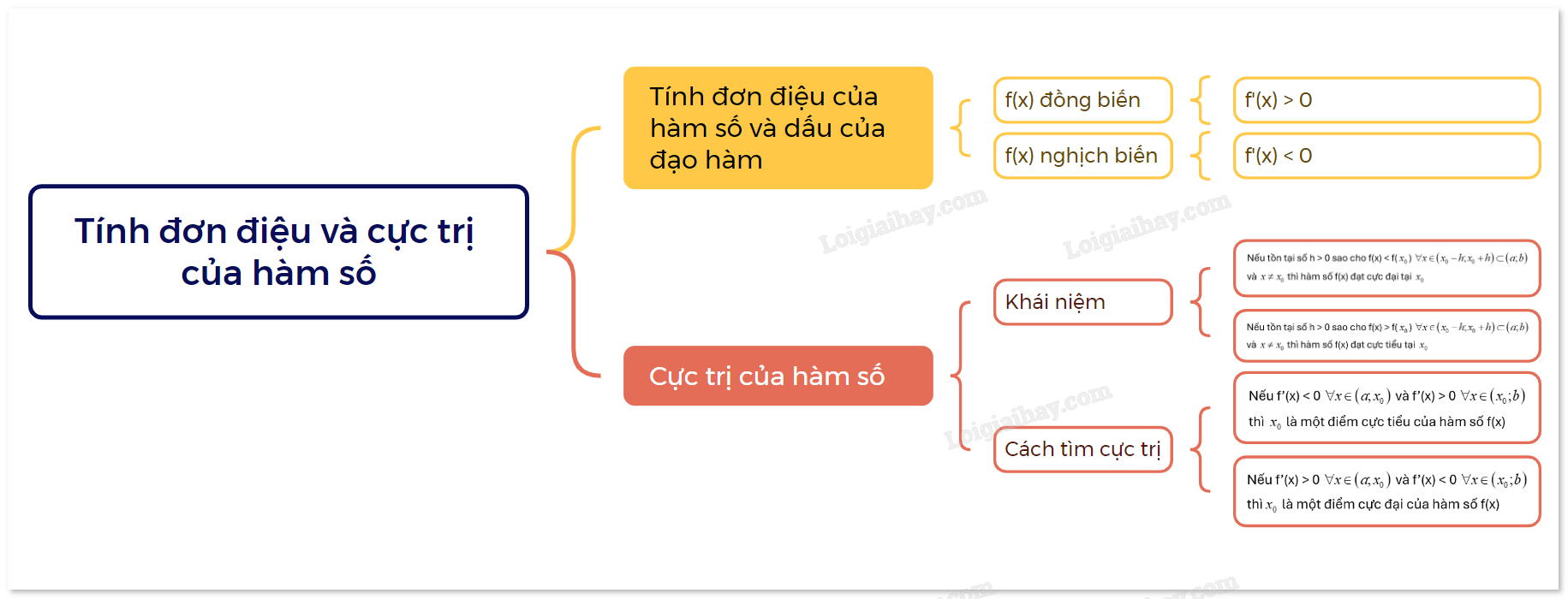
Tổng quát, ta có quy tắc tìm cực trị của hàm số y = f(x)
|
Bình luận
Chia sẻ
- Lý thuyết Tính đơn điệu và cực trị của hàm số của hàm số Toán 12 Cánh Diều
- Giải mục 1 trang 2,3,4 SGK Toán 12 tập 1 - Cùng khám phá
- Giải mục 2 trang 5,6,7 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.1 trang 8 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.2 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
