Bài 2. Phương trình bậc hai một ẩn - Toán 9 Cùng khám phá

Lý thuyết Phương trình bậc hai một ẩn Toán 9 Cùng khám phá

1. Phương trình bậc hai một ẩn Phương trình dạng $a{x^2} + bx + c = 0$ với a, b, c là ba số đã cho và $a \ne 0$ , được gọi là phương trình bậc hai một ẩn (ẩn số là x) hay còn nói gọn là phương trình bậc hai.

1. Phương trình bậc hai một ẩn

Phương trình dạng $a{x^2} + bx + c = 0$ với a, b, c là ba số đã cho và $a \ne 0$ , được gọi là phương trình bậc hai một ẩn (ẩn số là x) hay còn nói gọn là phương trình bậc hai.

Ví dụ: Phương trình $2{x^2} - 3x + 1 = 0$ là phương trình bậc hai với $a = 2;b = - 3;c = 1$ .

Phương trình ${x^2} - 3 = 0$ là phương trình bậc hai với $a = 1,b = 0,c = - 3$ .

Phương trình $0{x^2} - 2x - 3 = 0$ không là phương trình bậc hai vì $a = 0$ .

2. Một số cách giải phương trình bậc hai

Ta có thể giải phương trình $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$ theo các cách sau:

- Đưa về phương trình tích

- Biến đổi vế trái của phương trình về dạng $a{\left( {x + h} \right)^2} = k$ với h, k là các hằng số.

Ví dụ 1: Giải phương trình $2{x^2} - 4x = 0$

Ta có:

$\begin{array}{l}2{x^2} - 4x = 0\\2x\left( {x - 2} \right) = 0\end{array}$

$x = 0$ hoặc $x - 2 = 0$

$x = 0$ hoặc $x = 2$ .

Vậy phương trình có hai nghiệm ${x_1} = 0,{x_2} = 2$ .

Ví dụ 2: Giải phương trình ${x^2} - 4x = 1$

Ta có:

$\begin{array}{l}{x^2} - 4x = 5\\{x^2} - 4x + 4 = 5 + 4\\{\left( {x - 2} \right)^2} = 9\end{array}$

$x - 2 = 3$ hoặc $x - 2 = - 3$

suy ra $x = 5$ hoặc $x = - 1$ .

Vậy phương trình có hai nghiệm ${x_1} = 5,{x_2} = - 1$ .

3. Công thức nghiệm của phương trình bậc hai

Công thức nghiệm của phương trình bậc hai:

Cho phương trình $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$ và $\Delta = {b^2} - 4ac$ .

- Nếu $\Delta > 0$ thì phương trình có hai nghiệm phân biệt:

${x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}$ .

- Nếu $\Delta = 0$ thì phương trình có nghiệm kép ${x_1} = {x_2} = - \frac{b}{{2a}}$ .

- Nếu $\Delta < 0$ thì phương trình vô nghiệm.

Ví dụ: Giải phương trình ${x^2} - 7x - 8 = 0$ .

Ta có: $a = 1,b = - 7,c = - 8$ .

$\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.1.\left( { - 8} \right) = 81 > 0$ .

Vậy phương trình có hai nghiệm phân biệt là

${x_1} = \frac{{ - \left( { - 7} \right) + \sqrt {81} }}{{2.1}} = 8;{x_2} = \frac{{ - \left( { - 7} \right) - \sqrt {81} }}{{2.1}} = - 1$ .

Lưu ý: Nếu phương trình $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$ có $ac < 0$ (a và c trái dấu) thì $\Delta = {b^2} - 4ac > 0$ . Khi đó, phương trình có hai nghiệm phân biệt.

Ví dụ: Phương trình ${x^2} + 3572x - 3573 = 0$ có $a = 1 > 0,c = - 3573 < 0$ , suy ra a và c trái dấu.

Do đó phương trình có hai nghiệm phân biệt.

Công thức nghiệm thu gọn của phương trình bậc hai:

Cho phương trình $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$ có $b = 2b'$ , $\Delta ' = b{'^2} - ac$ .

- Nếu $\Delta ' > 0$ thì phương trình có hai nghiệm phân biệt:

${x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a}$ .

- Nếu $\Delta ' = 0$ thì phương trình có nghiệm kép ${x_1} = {x_2} = - \frac{{b'}}{a}$ .

- Nếu $\Delta ' < 0$ thì phương trình vô nghiệm.

Ví dụ: Giải phương trình $7{x^2} - 12x + 5 = 0$ .

Ta có: $a = 7,b' = - 6,c = 5$ .

$\Delta ' = b{'^2} - ac = {\left( { - 6} \right)^2} - 7.5 = 1 > 0$ .

Vậy phương trình có hai nghiệm phân biệt là

${x_1} = \frac{{ - \left( { - 6} \right) + 1}}{7} = 1;{x_2} = \frac{{ - \left( { - 6} \right) - 1}}{7} = \frac{5}{7}$ .

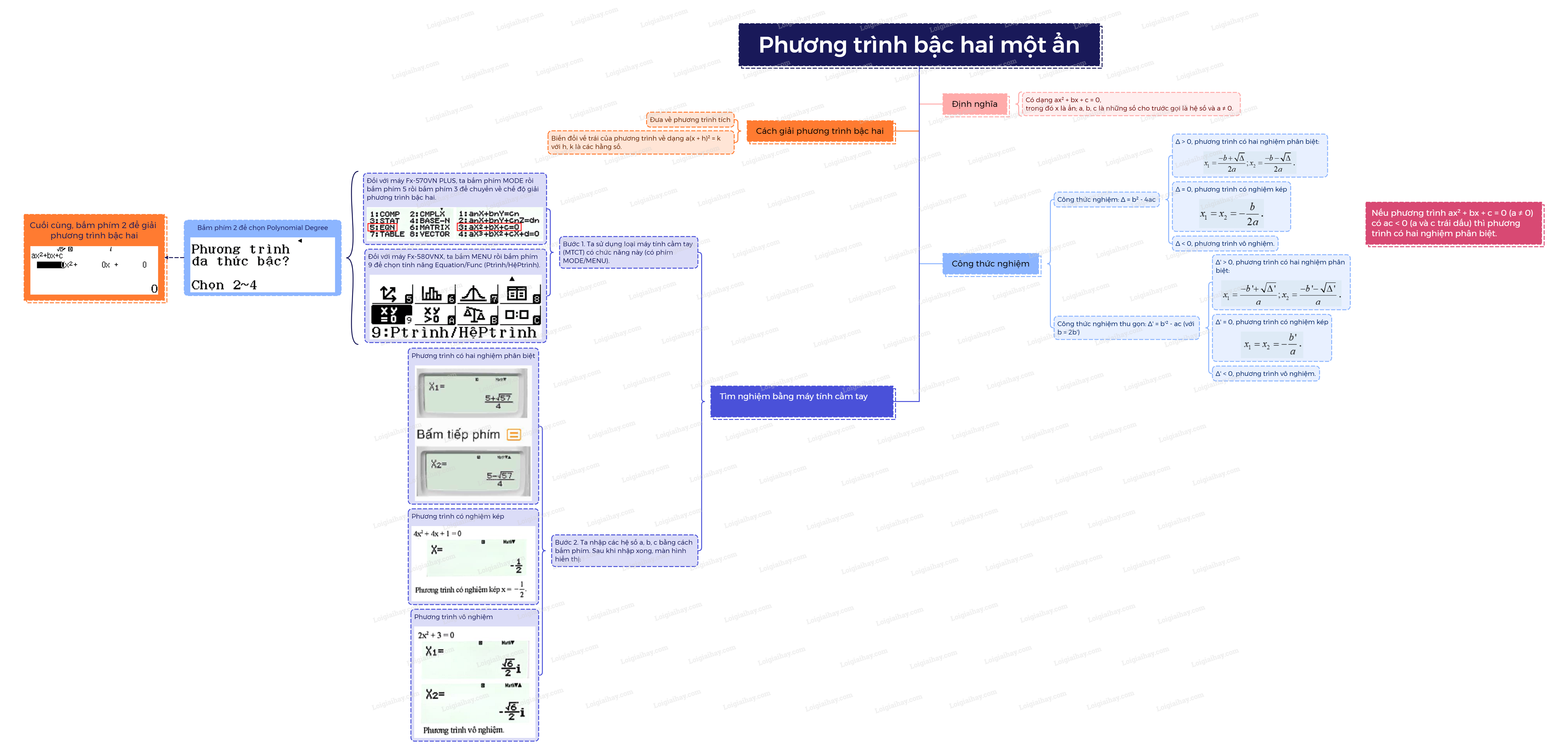
3. Tìm nghiệm của phương trình bậc hai bằng máy tính cầm tay

Sử dụng máy tính cầm tay, ta có thể dễ dạng tìm nghiệm của các phương trình bậc hai.

Bước 1. Ta sử dụng loại máy tính cầm tay (MTCT) có chức năng này (có phím MODE/MENU).

- Đối với máy Fx-570VN PLUS, ta bấm phím MODE rồi bấm phím 5 rồi bấm phím 3 để chuyển về chế độ giải phương trình bậc hai.

- Đối với máy Fx-580VNX, ta bấm MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).

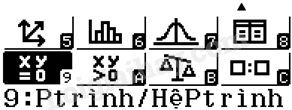
Bấm phím 2 để chọn Polynomial Degree

Cuối cùng, bấm phím 2 để giải phương trình bậc hai

Bước 2. Ta nhập các hệ số $a,b,c$ bằng cách bấm

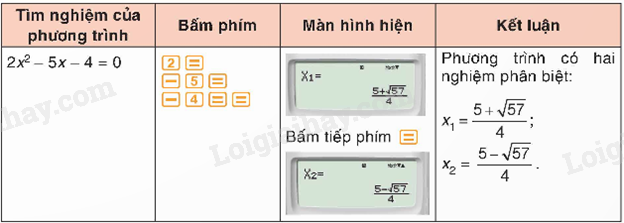
Đối với phương trình bậc hai có nghiệm kép, ta nhận được kết quả hiển thị trên màn hình như sau:

Đối với phương trình bậc hai vô nghiệm, ta nhận được kết quả hiển thị trên màn hình như sau:

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 7 SGK Toán 9 tập 2 - Cùng khám phá
Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?
Giải mục 2 trang 8, 9 SGK Toán 9 tập 2 - Cùng khám phá
Phân tích vế trái của các phương trình sau thành nhân tử rồi giải các phương trình đó: a) 2x – x2 = 0; b) ${x^2} - 6x + 9 = \frac{1}{2}$
Giải mục 3 trang 9, 10, 11 SGK Toán 9 tập 2 - Cùng khám phá
Biến đổi phương trình tổng quát ax2 + bx + c = 0 (a $\ne$ 0) theo các bước tương tự ví dụ 3, ta có: $\begin{array}{l}a{x^2} + bx + c = 0\\a{x^2} + bx = - c\\{x^2} + \frac{b}{a}x = \frac{{ - c}}{a}\\{x^2} + 2.x.\frac{b}{{2a}} + {\left( {\frac{b}{{2a}}} \right)^2} = \frac{{ - c}}{a} + {\left( {\frac{b}{{2a}}} \right)^2}\\{\left( {x + \frac{b}{{2a}}} \right)^2} = \frac{{{b^2} - 4ac}}{{4{a^2}}}.\end{array}$ Đặt $\Delta = {b^2} - 4ac$ và gọi là biệt thức của phương trình ( $\Delta$ là một
Giải mục 4 trang 13 SGK Toán 9 tập 2 - Cùng khám phá
Dùng máy tính cầm tay tính nghiệm (nếu có) của các phương trình sau (làm tròn kết quả đến hàng phần trăm): a) $11{x^2} + 4x - 189 = 0$ b) $2{x^2} - 8\sqrt 2 x + 16 = 0$ c) $\sqrt 2 {x^2} - \sqrt 3 x + 1 = 0$
Giải bài tập 6.8 trang 14 SGK Toán 9 tập 2 - Cùng khám phá
Đưa các phương trình sau về dạng $a{x^2} + bx + c = 0$ và chỉ rõ các hệ số a, b, c: a) ${x^2} - x = 3x + 1$ b) $3{x^2} - 4x = \sqrt 2 {x^2} - 2$ c) ${\left( {x + 1} \right)^2} = 2(x - 1)$ d) ${x^2} - m = 2(m + 1)x$ , m là một hằng số.
Giải bài tập 6.9 trang 14 SGK Toán 9 tập 2 - Cùng khám phá
Không giải các phương trình, hãy xác định số nghiệm của mỗi phương trình sau: a) $6{x^2} - 2x + 9 = 0$ b) $3{x^2} - 2\sqrt {15} x + 5 = 0$ c) $\frac{1}{3}{y^2} - 5y + \frac{3}{2} = 0$ d) $2,3{t^2} + 1,15t - 6,4 = 0$
Giải bài tập 6.10 trang 14 SGK Toán 9 tập 2 - Cùng khám phá
Giải các phương trình sau: a) ( - 2{x^2} + x + 1 = 0) b) ({x^2} - x + 4 = 0) c) (4{x^2} - 4x + 1 = 0) d) ( - {x^2} - 4x + 1 = 0) e) ({y^2} - y - 3 = 0) g) ({z^2} - 2sqrt 5 z + 5 = 0)
Giải bài tập 6.11 trang 14 SGK Toán 9 tập 2 - Cùng khám phá
Tìm các giá trị của m để phương trình ${x^2} - (m + 3)x + {m^2} = 0$ có nghiệm x = 1.
Giải bài tập 6.12 trang 14 SGK Toán 9 tập 2 - Cùng khám phá
Giải các phương trình sau: a) ${x^2} - x - 1 = 3x + 1$ b) $\frac{{{x^2} - 9}}{3} + 2 = x(1 - x)$ c) ${\left( {x + 2} \right)^2} - 3(x + 2) + 2 = 0$ d) $2{x^4} + 3{x^2} - 2 = 0$
Giải bài tập 6.13 trang 14 SGK Toán 9 tập 2 - Cùng khám phá
Lượng nhiên liệu tiêu thụ y (l/100 km) của một số loại ô tô phụ thuộc vào tốc độ di chuyển x (km/h) theo hàm số $y = \frac{1}{{320}}{x^2} - \frac{3}{8}x + \frac{{73}}{4}$ với $20 \le x \le 140$ . Hỏi ô tô đi với tốc độ nào thì lượng nhiên liệu tiêu thụ là 7 l/100 km?

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com

>> Chi tiết khoá học xem: TẠI ĐÂY

Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.