 Toán 9 kết nối tri thức | Giải toán lớp 9 kết nối tri thức
Toán 9 kết nối tri thức | Giải toán lớp 9 kết nối tri thức
 Bài 14. Cung và dây của một đường tròn - Toán 9 Kết nối..
Bài 14. Cung và dây của một đường tròn - Toán 9 Kết nối..
Giải mục 1 trang 87, 88 SGK Toán 9 tập 1 - Kết nối tri thức
Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
HĐ
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động trang 87 SGK Toán 9 Kết nối tri thức
Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
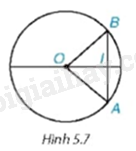
Phương pháp giải:
Áp dụng bất đẳng thức tam giác đối với tam giác AOB.
Lời giải chi tiết:
Xét tam giác AOB có: AB < OA + OB (bất đẳng thức tam giác)
mà OA = OB = R nên AB < 2R.
LT1
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 88 SGK Toán 9 Kết nối tri thức
Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên đường tròn, ta đều có: BC < AB + AC < 2BC
Phương pháp giải:
- Áp dụng bất đẳng thức trong tam giác ta có: BC < AB + AC.
- Theo quan hệ giữa dây và đường kính ta có: AB < BC, AC < BC
Do đó: AB + AC < 2BC.
Lời giải chi tiết:
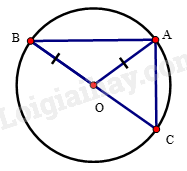
Xét tam giác ABC có: BC < AB + AC (bất đẳng thức tam giác) (1)
Xét đường tròn đường kính BC có dây cung AB, AC ta có: AB < BC, AC < BC
Suy ra: AB + AC < 2BC (2)
Từ (1) và (2) suy ra: BC < AB + AC < 2BC.
- Giải mục 2 trang 89, 90 SGK Toán 9 tập 1 - Kết nối tri thức
- Giải bài tập 5.5 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
- Giải bài tập 5.6 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
- Giải bài tập 5.7 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
- Giải bài tập 5.8 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục











