Giải bài tập 2.18 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức

Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có (Aleft( {1;1; - 1} right),Bleft( {0;3;0} right),C'left( {2; - 3;6} right)). a) Xác định tọa độ của điểm C. b) Xác định các tọa độ đỉnh còn lại của hình hộp.

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Trong không gian Oxyz, cho hình hộp OABC.O’A’B’C’ có \(A\left( {1;1; - 1} \right),B\left( {0;3;0} \right),C'\left( {2; - 3;6} \right)\).

a) Xác định tọa độ của điểm C.

b) Xác định các tọa độ đỉnh còn lại của hình hộp.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về tọa độ của vectơ theo tọa độ hai đầu mút để tìm tọa độ vectơ: Trong không gian Oxyz, cho hai điểm \(M\left( {{x_M},{y_M},{z_M}} \right)\) và \(N\left( {{x_N};{y_N};{z_N}} \right)\).

Khi đó, \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M}} \right)\).

Lời giải chi tiết

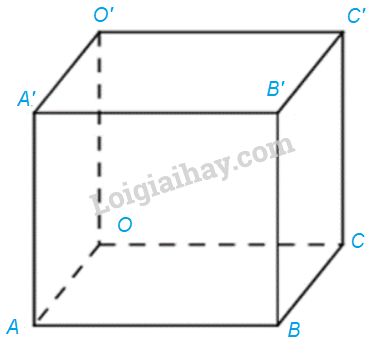
a) Ta có: O(0; 0; 0).

Vì OABC.O’A’B’C’ là hình hộp nên AOBC là hình bình hành. Do đó:

\(\overrightarrow {OA} = \overrightarrow {CB} \Rightarrow \left\{ \begin{array}{l}{x_A} = {x_B} - {x_C}\\{y_A} = {y_B} - {y_C}\\{z_A} = {z_B} - {z_C}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_C} = {x_B} - {x_A} = -1\\{y_C} = {y_B} - {y_A} = 2\\{z_C} = {z_B} - {z_A} = 1\end{array} \right. \Rightarrow C\left( {-1; 2; 1} \right)\).

b) \(\overrightarrow {CC'} = (3; - 5;5)\).

Vì OABC.O’A’B’C’ là hình hộp nên:

\(\overrightarrow {OO'} = \overrightarrow {CC'} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{O'}} = 3}\\{{y_{O'}} = - 5}\\{{z_{O'}} = 5}\end{array}} \right. \Rightarrow O'\left( {3; - 5;5} \right)\).

\(\overrightarrow {AA'} = \overrightarrow {CC'} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} - 1 = 3}\\{{y_{A'}} - 1 = - 5}\\{{z_{A'}} - ( - 1) = 5}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{A'}} = 4}\\{{y_{A'}} = - 4}\\{{z_{A'}} = 4}\end{array}} \right. \Rightarrow A'\left( {4; - 4;4} \right)\).

\(\overrightarrow {BB'} = \overrightarrow {CC'} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{B'}} - 0 = 3}\\{{y_{B'}} - 3 = - 5}\\{{z_{B'}} - 0 = 5}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{x_{B'}} = 3}\\{{y_{B'}} = - 2}\\{{z_{B'}} = 5}\end{array}} \right. \Rightarrow B'\left( {3; - 2;5} \right)\).

Bình luận

Chia sẻ

Bình chọn:

3.3 trên 4 phiếu

Bài tiếp theo

Giải bài tập 2.19 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.
Giải bài tập 2.17 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O và các đỉnh D, B, A’ có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.
Giải bài tập 2.16 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau: a) A trùng với gốc tọa độ; b) A nằm trên tia Ox và \(OA = 2\); c) A nằm trên tia đối của tia Oy và \(OA = 3\).
Giải bài tập 2.15 trang 65 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, xác định tọa độ của vectơ \(\overrightarrow {AB} \) trong mỗi trường hợp sau: a) \(A\left( {0;0;0} \right)\) và \(B\left( {4;2; - 5} \right)\); b) \(A\left( {1; - 3;7} \right)\) và \(B\left( {1; - 3;7} \right)\); c) \(A\left( {5;4;9} \right)\) và \(B\left( { - 5;7;2} \right)\).
Giải bài tập 2.14 trang 64 SGK Toán 12 tập 1 - Kết nối tri thức
Hãy mô tả hệ tọa độ Oxyz trong căn phòng ở Hình 2.44 sao cho gốc O trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng (Oxy) và mặt trần nhà trùng với mặt phẳng (Oxz).
Giải bài tập 2.13 trang 64 SGK Toán 12 tập 1 - Kết nối tri thức
Trong không gian Oxyz, cho ba vectơ (overrightarrow a ), (overrightarrow b ), (overrightarrow c ) đều khác (overrightarrow 0 ) và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng? a) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lần lượt song song với giá của các vectơ (overrightarrow a ), (overrightarrow b ), (overrightarrow c ). b) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lần lượt trùng với giá của các vectơ (overrightarrow a ), (over
Giải mục 2 trang 61, 62, 63 SGK Toán 12 tập 1 - Kết nối tri thức
Tọa độ của điểm, tọa độ của vectơ trong không gian
Giải mục 1 trang 60, 61 SGK Toán 12 tập 1 - Kết nối tri thức
Hệ trục tọa độ trong không gian
Giải câu hỏi mở đầu trang 60 SGK Toán 12 tập 1 - Kết nối tri thức
Trong Hình 2.34, một chiếc bóng đèn được treo cách sàn nhà là 2 m, cách hai bức tường lần lượt là 1 m và 1,5 m. Kiến thức toán học nào giúp mô tả chính xác và ngắn gọn vị trí của chiếc bóng đèn trong không gian?
Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Kết nối tri thức
1. Hệ trục tọa độ trong không gian