Giải bài 9.46 trang 111 SGK Toán 8 tập 2 - Kết nối tri thức

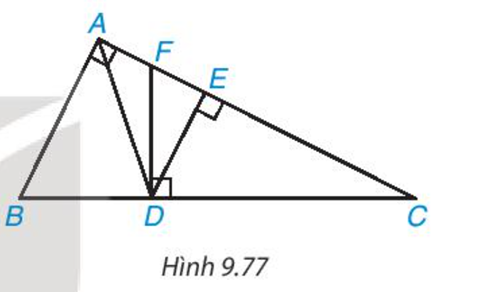
Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77

Đề bài

Cho tam giác ABC vuông tại A và các điểm D, E, F như Hình 9.77 sao cho AD là phân giác của góc BAC, DE và DF lần lượt vuông góc với AC và BC . Chứng minh rằng:

a) $\frac{{B{\rm{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}$, từ đó suy ra $A{\rm{E}} = \frac{{AB.AC}}{{AB + AC}}$

b) ΔDFC ∽ ΔABC

c) DF=DB

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng các tam giác đồng dạng để chứng minh

Lời giải chi tiết

a) Vì AD là tia phân giác của góc BAC nên $\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}$ suy ra $DB.AC = DC.AB(*)$

Ta có: $B{{D}}.\left( {AB + AC} \right)$$ = B{{D}}.AB + B{{D}}.AC$

$\begin{array}{l} = DB.AB + DC.AB\\ = AB.\left( {DB + DC} \right) = AB.BC\end{array}$

Do đó $B{{D}}.\left( {AB + AC} \right) = AB.BC$ suy ra $\frac{{B{{D}}}}{{BC}} = \frac{{AB}}{{AB + AC}}(1)$

Xét $\Delta CE{{D}}$ và $\Delta CAB$ có:

$\widehat C\,chung$

$\widehat A = \widehat E$

nên $\Delta CE{D}\backsim \Delta CAB$ (g.g)

Suy ra $\frac{{CE}}{{CA}} = \frac{{C{{D}}}}{{CB}}$

$\begin{array}{l}\frac{{AC - A{{E}}}}{{AC}} = \frac{{BC - B{{D}}}}{{BC}}\\1 - \frac{{A{{E}}}}{{AC}} = 1 - \frac{{DB}}{{BC}}\\\frac{{A{{E}}}}{{AC}} = \frac{{DB}}{{BC}}(2)\end{array}$

Từ (1), (2) suy ra: $\frac{{A{{E}}}}{{AC}} = \frac{{AB}}{{AB + AC}}$ nên $A{{E}} = \frac{{AB.AC}}{{AB + AC}}$

b) Xét $\Delta DFC$ và $\Delta ABC$ có:

$\widehat {FDC} = \widehat {BAC}\left( { = 90^\circ } \right)$

$\widehat C\,chung$

suy ra $\Delta DFC\backsim \Delta ABC$. (g.g)

c) Từ $\Delta DFC\backsim \Delta ABC$ suy ra $\frac{{DF}}{{AB}} = \frac{{DC}}{{AC}}$

nên $DF = \frac{{AB.DC}}{{AC}}(3)$

Từ (*) ta có: $DB = \frac{{DC.AB}}{{AC}}(4)$

Từ (3), (4) suy ra: DF = DB