-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
Giải bài 54 trang 124 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB < AC. Gọi M là trung điểm của đoạn thẳng BC. Trên cung BC không chứa điểm A, lấy điểm D sao cho \(\widehat {BAD} = \widehat {CAM}\). a) Chứng minh \(\widehat {ADB} = \widehat {CDM}\). b) Gọi E là giao điểm của tia OM và cung BC. Tính diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE theo R, biết \(BC = R\sqrt 2 \).
Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB < AC. Gọi M là trung điểm của đoạn thẳng BC. Trên cung BC không chứa điểm A, lấy điểm D sao cho \(\widehat {BAD} = \widehat {CAM}\).
a) Chứng minh \(\widehat {ADB} = \widehat {CDM}\).
b) Gọi E là giao điểm của tia OM và cung BC. Tính diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE theo R, biết \(BC = R\sqrt 2 \).
Phương pháp giải - Xem chi tiết
a) Bước 1: Chứng minh\(\widehat {BAM} = \widehat {DAC}\).
Bước 2: Chứng minh \(\frac{{AB}}{{AD}} = \frac{{CM}}{{CD}}\) (\(\Delta ABM\backsim \Delta ADC\)).
Bước 3: Chứng minh \(\widehat {ADB} = \widehat {CDM}\) (\(\Delta ABD\backsim \Delta CMD\)).
b) Bước 1: Chứng minh \(\Delta OBM = \Delta OCM\)để tính CM và suy ra \(\widehat {OMB} = \widehat {OMC}\).
Bước 2: Tính OM, chứng minh tam giác OCM vuông cân tại M.
Bước 3: Áp dụng công thức \(S = \frac{{\pi {R^2}n}}{{360}}\).
Lời giải chi tiết
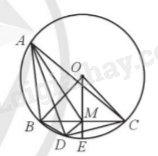
a) Ta có \(\widehat {BAD} + \widehat {DAM} = \widehat {BAM},\widehat {DAM} + \widehat {CAM} = \widehat {DAC}\), mà \(\widehat {BAD} = \widehat {CAM}\)suy ra \(\widehat {BAM} = \widehat {DAC}\).
Ta lại có \(\widehat {ABM} = \widehat {ADC}\) (2 góc nội tiếp chắn cung AC của (O))
Xét tam giác ABM và tam giác ADC có:
\(\widehat {ABM} = \widehat {ADC}\), \(\widehat {BAM} = \widehat {DAC}\)
Suy ra \(\Delta ABM\backsim \Delta ADC\)(g.g), do đó \(\frac{{AB}}{{AD}} = \frac{{BM}}{{CD}} = \frac{{CM}}{{CD}}\).
Xét tam giác ABD và tam giác CMD có:
\(\widehat {BAD} = \widehat {MCD}\) (góc nội tiếp cùng chắn cung BD của (O))
\(\frac{{AB}}{{AD}} = \frac{{CM}}{{CD}}\)
Suy ra \(\Delta ABD\backsim \Delta CMD\)(c.g.c), do đó \(\widehat {ADB} = \widehat {CDM}\).
b) Xét tam giác OBM và tam giác OCM có:
OM chung
\(OB = OC\)(bằng bán kính (O))
\(MB = MC\)(M là trung điểm của BC)
Suy ra \(\Delta OBM = \Delta OCM\)(c.c.c), do đó \(CM = \frac{{BC}}{2} = \frac{{R\sqrt 2 }}{2}\) và \(\widehat {OMB} = \widehat {OMC}\)
Mà \(\widehat {OMB} + \widehat {OMC} = 180^\circ \), suy ra \(\widehat {OMB} = \widehat {OMC} = \frac{{180^\circ }}{2} = 90^\circ \)
Áp dụng định lý Pythagore trong tam giác vuông OCM có:
\(OM = \sqrt {O{C^2} - C{M^2}} = \sqrt {{R^2} - {{\left( {\frac{{R\sqrt 2 }}{2}} \right)}^2}} = \frac{{R\sqrt 2 }}{2}\)
Ta thấy \(OM = CM\left( { = \frac{{R\sqrt 2 }}{2}} \right)\) nên tam giác OCM vuông cân tại M, suy ra \(\widehat {COE} = 45^\circ \).
Diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE là:
\(S = \frac{{\pi {R^2}.45}}{{360}} = \frac{{\pi {R^2}}}{8}\) (đvdt).
Bình luận
Chia sẻ
- Giải bài 55 trang 124 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 56 trang 124 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 57 trang 124 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 58 trang 125 sách bài tập toán 9 - Cánh diều tập 1
- Giải bài 59 trang 125 sách bài tập toán 9 - Cánh diều tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
