Giải Bài 3 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo

Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.

Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên...

Đề bài

Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.

a) Chứng minh rằng AD = AC.

b) Chứng minh rằng \(\widehat {ADH} = \widehat {BAH}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Ta chứng minh tam giác ACD cân tại A sau đó suy ra AC = AD

b) Ta chứng minh \(\widehat {BAH} + \widehat {HAC} = {90^o} = \widehat {HAC} + \widehat {HCA}\) và \(\widehat D = \widehat C\)

Lời giải chi tiết

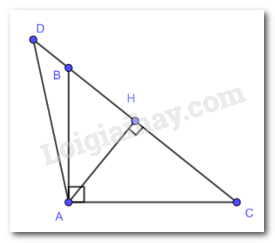
a) Xét \(\Delta AHD\) và \(\Delta AHC\) có :

AH chung

DH = HC ( C đối xứng D qua H)

\(\widehat {AHD} = \widehat {AHC} = {90^o}\)

nên \(\Delta AHD = \Delta AHC(c - g - c)\)

suy ra \(AD = AC\)(cạnh tương ứng)

Do đó \(\Delta ADC\) cân tại A suy ra \(\widehat C = \widehat D\) (góc tương ứng) (1)

b) Ta có \(\widehat {BAH} + \widehat {HAC} = {90^o}\) và \(\widehat {HCA} + \widehat {HAC} = {90^o}\)

nên \(\widehat {BAH} = \widehat {HCA}\) (2)

Từ (1) và (2) suy ra \(\widehat {ADH} = \widehat {BAH}\)

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Giải Bài 4 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN
Giải Bài 5 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác nhọn ABC (AB < AC), vẽ đường cao AH. Đường trung trực của BC cắt AC tại M, cắt BC tại N.
Giải Bài 6 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.
Giải Bài 7 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC vuông tại A
Giải Bài 8 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Ở Hình 1, cho biết AE = AF và.
Giải Bài 9 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB ở M. Từ B kẻ BH vuông góc với đường thẳng CM (H ∈ CM). Trên tia đối của tia HC lấy điểm E sao cho HE = HM.
Giải Bài 10 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Trên đường thẳng a lấy ba điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.
Giải Bài 2 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.
Giải Bài 1 trang 84 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC cân tại A