-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
-
Chương VI. Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập và phân loại dữ liệu
- Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
- Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
- Bài tập cuối chương VI
-
Chương VII. Phương trình bậc nhất một ẩn
-
Chương VIII. Tam giác đồng dạng. Hình đồng dạng
- Bài 1. Định lí Thalès trong tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 9. Hình đồng dạng
- Bài tập cuối chương VIII
-
Giải bài 26 trang 99 sách bài tập toán 8 - Cánh diều
Cho hình thoi \(ABCD\) có góc \(B\) tù. Kẻ \(BE\) vuông góc \(AD\) tại \(E\), \(BF\) vuông góc với \(CD\) tại \(F\).
Tổng hợp đề thi giữa kì 1 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho hình thoi \(ABCD\) có góc \(B\) tù. Kẻ \(BE\) vuông góc \(AD\) tại \(E\), \(BF\) vuông góc với \(CD\) tại \(F\). Gọi \(M,N\) lần lượt là giao điểm của \(BE,BF\) với \(AC\). Chứng minh tứ giác \(BMDN\) là hình thoi.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của hình thoi:
Trong một hình thoi:
- Các cạnh đối song song
- Các góc đối bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
Lời giải chi tiết
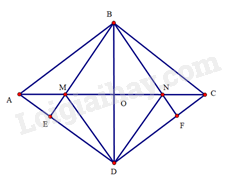
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
Do \(ABCD\) là hình thoi nên \(AC\) vuông góc với \(BD\) tại trung điểm \(O\) của \(BD\). Suy ra \(AC\) là đường trung trực của \(BD\). Do đó \(BM = DM,BN = DN\).
Do \(ABCD\) là hình thoi nên \(BA = BC,\widehat {BAE} = \widehat {BCF}\).
Suy ra \(\Delta ABE = \Delta BCF\) (cạnh huyền – góc nhọn kề)
Do đó \(\widehat {ABE} = \widehat {CBF}\). Mà \(\widehat {ABD} = \widehat {CBD}\), suy ra \(\widehat {MBO} = \widehat {NBO}\).
\(\Delta MBO = \Delta NBO\) (cạnh góc vuông – góc nhọn). suy ra \(BM = BN\)
Mà \(BM = DM\) và \(BN = DN\), suy ra \(BM = DM = BN = DN\).
Tứ giác \(BMDN\) có \(BM = DM = BN = DN\) nên \(BMDN\) là hình thoi.
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
