-
GIẢI SGK TOÁN 11 CÁNH DIỀU - MỚI NHẤT
-
Toán 10 tập 1 - Cánh diều
-
Toán 10 tập 2 - Cánh diều
Giải bài 2 trang 29 SGK Toán 10 tập 1 – Cánh diều
Biểu diễn miền nghiệm của hệ bất phương trình:
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Biểu diễn miền nghiệm của hệ bất phương trình:
a) \(\left\{ \begin{array}{l}x + 2y < - 4\\y \ge x + 5\end{array} \right.\)
b) \(\left\{ \begin{array}{l}4x - 2y > 8\\x \ge 0\\y \le 0\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Bước 1: Vẽ các đường thẳng.
Bước 2: Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Bước 3: Phần không bị gạch là miền nghiệm.
Lời giải chi tiết
a) Vẽ các đường thẳng \(x + 2y = - 4\)(nét đứt) và \(y = x + 5\) (nét liền)
Thay tọa độ O vào \(x + 2y < - 4\) ta được: \(0 + 2.0 < - 4\) (Sai)
=> Gạch đi phần chứa O.
Thay tọa độ O vào \(y \ge x + 5\) ta được: \(0 \ge 0 + 5\) (Sai)
=> Gạch đi phần chứa O.
\(x + 2y = -4 => y = \frac{-4 - x}{2} \)
Xét phương trình hoành độ giao điểm của hai đường thẳng \(x + 2y = - 4\) và \(y = x + 5\), ta được:
\( \frac{-4 - x}{2} = x + 5 \\ x = \frac{-14}{3} \\ => y = \frac{1}{3} \)
Miền nghiệm của hệ:
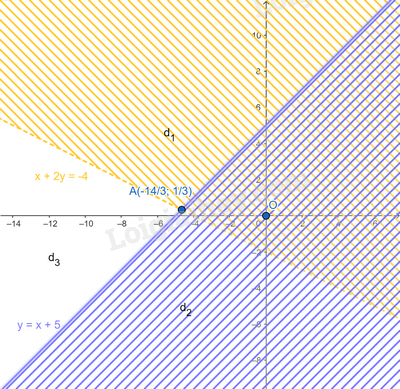
Từ hình vẽ ta thấy miền nghiệm của hệ là \(d_3\)
b) Vẽ các đường thẳng \(4x - 2y = 8\)(nét đứt) và hai trục (nét liền)
Thay tọa độ O vào \(4x - 2y > 8\) ta được: \(4.0 - 2.0 > 8\) (Sai)
=> Gạch đi phần chứa O.
Với \(x \ge 0\) thì gạch phần bên trái Oy
Với \(y \le 0\) thì gạch bên trên Ox
Miền nghiệm của hệ:
Bình luận
Chia sẻ
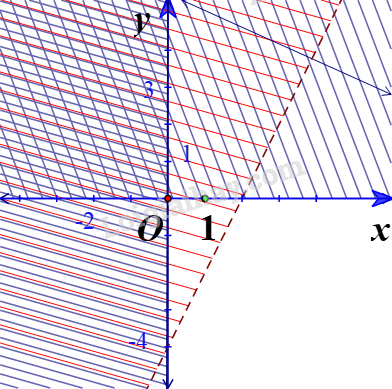
- Giải bài 3 trang 29 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 4 trang 29 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 1 trang 29 SGK Toán 10 tập 1 – Cánh diều
- Giải mục II trang 26, 27 SGK Toán 10 tập 1 - Cánh diều
- Giải mục I trang 25, 26 SGK Toán 10 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
