Giải bài 1.2 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1

Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau: a) (3x - 2y = 5); b) (0x + 2y = 4); c) (2x + 0y = - 3).

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) \(3x - 2y = 5\);

b) \(0x + 2y = 4\);

c) \(2x + 0y = - 3\).

Phương pháp giải - Xem chi tiết

+ Từ phương trình đầu bài cho, ta tính x theo y hoặc y theo x, từ đó kết luận được nghiệm tổng quát của phương trình.

+ Biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn là đường thẳng \(ax + by = c\).

Lời giải chi tiết

a) Vì \(3x - 2y = 5\) nên \(y = \frac{{3x - 5}}{2}\).

Do đó, nghiệm tổng quát của phương trình là \(\left( {x;\frac{{3x - 5}}{2}} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Đường thẳng d: \(3x - 2y = 5\) đi qua hai điểm A(0; -2,5) và \(B\left( {\frac{5}{3};0} \right)\).

Do đó, hình biểu diễn tất cả các nghiệm của mỗi phương trình đã cho là:

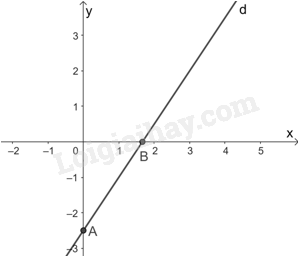
b) Vì \(0x + 2y = 4\) nên \(y = 2\).

Do đó, nghiệm tổng quát của phương trình là: \(\left( {x;2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm (0; 2).

Đó là đường thẳng d: \(y = 2\).

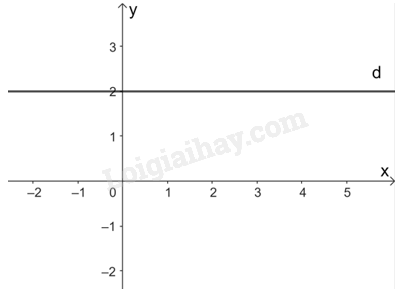
c) Vì \(2x + 0y = - 3\) nên \(x = - 1,5\).

Do đó, nghiệm tổng quát của phương trình là \(\left( { - 1,5;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.

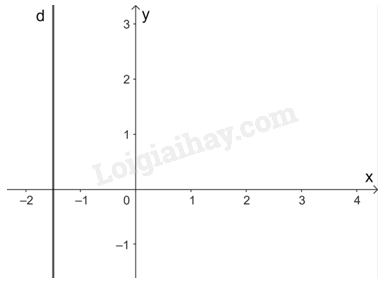
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm (-1,5; 0).

Đó là đường thẳng d: \(x = - 1,5\).

Bình luận

Chia sẻ

Bình chọn:

4 trên 5 phiếu

Bài tiếp theo

Giải bài 1.3 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho phương trình bậc nhất hai ẩn (mx + y = - 2). a) Xác định m để cặp số (1; -2) là một nghiệm của phương trình đã cho. b) Viết công thức nghiệm tổng quát của phương trình với m tìm được ở câu a.
Giải bài 1.4 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1
Bác Hương bán hàng tạp hóa và có (đủ nhiều) các tờ tiền lẻ loại 2 nghìn đồng và 5 nghìn đồng. Bác cần trả lại cho một người mua hàng 25 nghìn đồng. a) Gọi x là số tờ tiền loại 2 nghìn đồng, y là số tờ tiền loại 5 nghìn đồng mà bác Hương cần trả lại cho khách (left( {x,y in mathbb{N}} right)). Hãy lập phương trình bậc nhất hai ẩn đối với x và y. b) Hãy chỉ ra một nghiệm (x; y) với (x,y in mathbb{N}) của phương trình lập ở câu a để tìm một phương án trả lại tiền thừa cho khách giúp bá
Giải bài 1.5 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1
Một đội công nhân cần phải lắp đường ống dẫn nước trên một đoạn phố thẳng dài 65m. Có hai loại ống dài 3m và 5m. Hãy chỉ ra ít nhất hai phương án lắp ống để không cần phải cưa ống ra (coi rằng các mối nối là không đáng kể).
Giải bài 1.6 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho các cặp số (-2; 2), (1; 1), (4; 1), (8; -2) và hai phương trình: (x + 3y = 4); (1) (2x - 5y = - 3). (2) a) Những cặp số nào là nghiệm của phương trình (1)? b) Cặp số nào là nghiệm của hệ gồm hai phương trình (1) và phương trình (2)? c) Vẽ hai đường thẳng (d:x + 3y = 4) và (d':2x - 5y = - 3) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Giải bài 1.7 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1
Tìm a và b để hai phương trình (ax - 2y = 1) và (x + by = 3) nhận cặp số (1; -2) làm nghiệm chung.
Giải bài 1.8 trang 8 sách bài tập toán 9 - Kết nối tri thức tập 1
Bằng cách vẽ các đường thẳng thích hợp trên cùng một mặt phẳng tọa độ, hãy tìm nghiệm của mỗi hệ phương trình sau: a) (left{ begin{array}{l}2x = - 4\3x - y = 5end{array} right.); b) (left{ begin{array}{l}x - 2y = 4\2y = - 3end{array} right.).
Giải bài 1.1 trang 7 sách bài tập toán 9 - Kết nối tri thức tập 1
Giả sử (x; y) là nghiệm của phương trình bậc nhất hai ẩn (4x - 2y = 6.) a) Hoàn thành bảng sau đây: Từ đó suy ra 5 nghiệm của phương trình đã cho. b) Biểu diễn y theo x. Từ đó cho biết phương trình đã cho có bao nhiêu nghiệm?