Giải bài 12 trang 63 sách bài tập toán 8 – Cánh diều

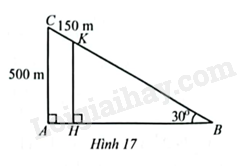
Một con dốc có độ nghiêng \(30^\circ \) so với mặt đất bằng phẳng. Đỉnh con dốc có độ cao \(CA\) là 500 m (Hình 17).

Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Cánh diều

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

Một con dốc có độ nghiêng \(30^\circ \) so với mặt đất bằng phẳng. Đỉnh con dốc có độ cao \(CA\) là 500 m (Hình 17). Một người di chuyển trên dốc, khi đến vị trí \(K\), cách đỉnh dốc 150 m thì người đó đang ở độ cao \(KH\) bằng bao nhiêu?

Phương pháp giải - Xem chi tiết

Áp dụng định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết

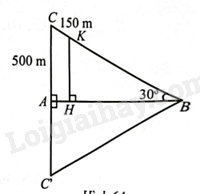
Trên tia đối của tia \(AC\) lấy \(C'\) sao cho \(AC' = AC\). Khi đó \(\Delta ACB = \Delta AC'B\) (c.g.c) nên \(BC = BC'\). Tam giác \(BCC'\) có \(BC = BC'\) và \(\widehat {CBC'} = 60^\circ \) nên là tam giác đều.

Suy ra \(CB = CC' = 2.CA = 2.500 = 1000\) (m)

Do đó \(KB = CB - CK = 1000 - 150 = 850\) (m)

Do \(KH//CA\) nên theo hệ quả của định lí Thales, ta có: \(\frac{{KB}}{{CB}} = \frac{{KH}}{{CA}}\) hay \(\frac{{850}}{{1000}} = \frac{{KH}}{{500}}\). Suy ra \(KH = 425\) m.

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài tiếp theo

Giải bài 13 trang 63 sách bài tập toán 8 – Cánh diều
Một ngôi nhà có thiết kế mái như Hình 18 và có các số đo như sau: \(AD = 1,5\) m, \(DE = 2,5\) m, \(BF = CG = 1\) m, \(FG = 5,5\) m. Tính chiều dài \(AB\) của mái nhà, biết \(DE//BC\).
Giải bài 11 trang 62 sách bài tập toán 8 – Cánh diều
Ở một nhà máy, người ta dùng một băng chuyền để chuyển nguyên vật liệu. Ba vòng quay \(A,B,C\) của băng chuyền đặt cách mặt đất ở các độ cao lần lượt là \(AH = 5\) (m), \(CI = 8\) (m), \(BK = x\) (m) (Hình 16).
Giải bài 10 trang 62 sách bài tập toán 8 – Cánh diều
Trong công viên có một dẻo đất có dạng hình tam giác \(MCD\) được mô tả như Hình 15. Giữa hai điểm \(A,B\) là một hồ nước sâu và một con đường đi bộ giữa \(C\) và \(D\).