 Đường tiệm cận của đồ thị hàm số - Từ điển môn Toán 12
Đường tiệm cận của đồ thị hàm số - Từ điển môn Toán 12 Đường tiệm cận là gì? Cách nhận biết đường tiệm cận đứng, tiệm cận ngang, tiệm cận xiên - Toán 12
1. Tiệm cận đứng là gì?
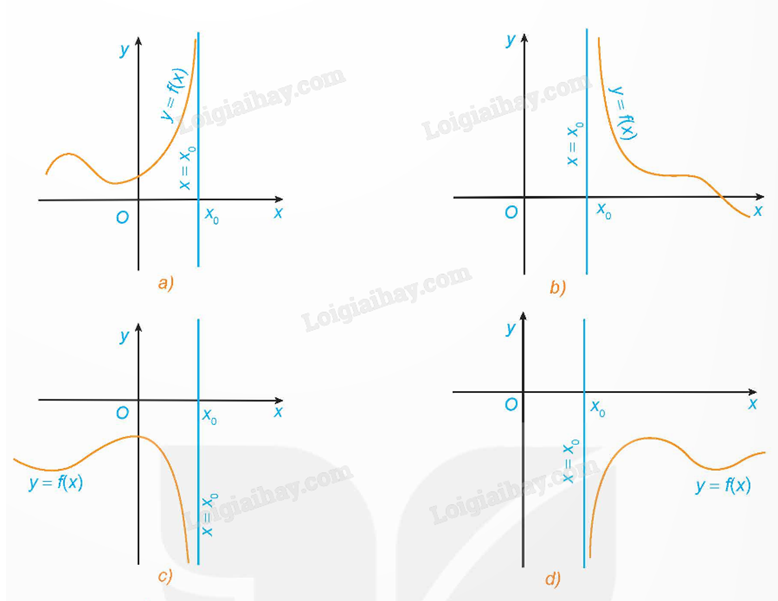
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thoả mãn:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \).
2. Tiệm cận ngang là gì?
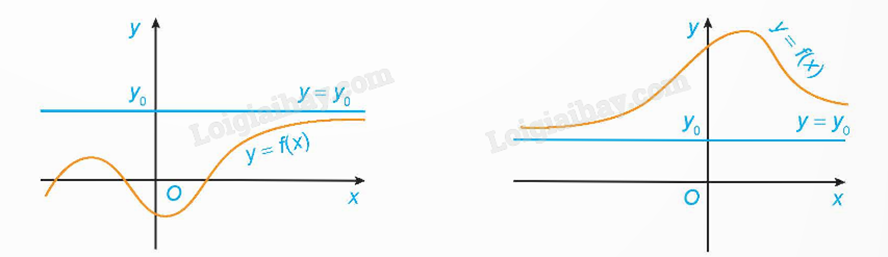
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
3. Đường tiệm cận xiên là gì?
Đường thẳng y = ax + b \((a \ne 0)\) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
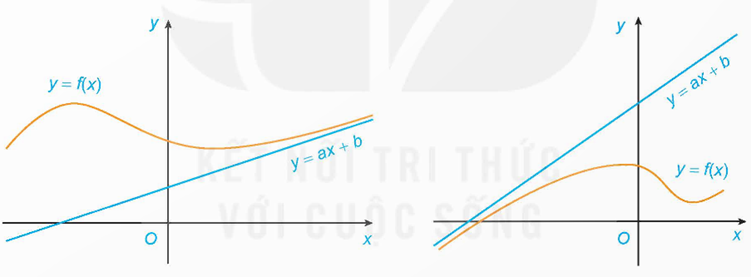
4. Cách nhận biết đường tiệm cận
a)
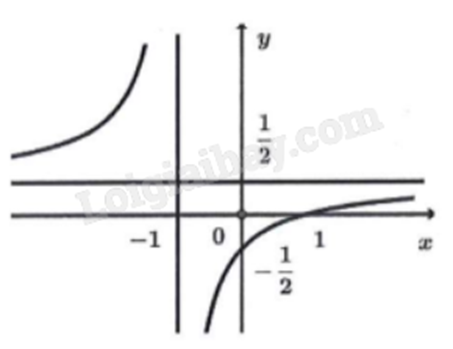
Tiệm cận ngang của đồ thị hàm số trên là \(y = \frac{1}{2}\).
Tiệm cận đứng của đồ thị hàm số trên là \(x = -\frac{1}{2}\).
b)
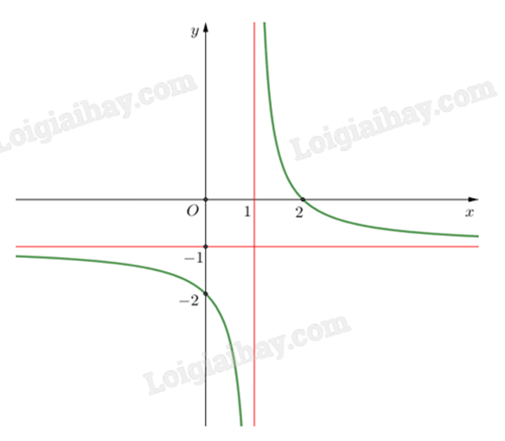
Tiệm cận đứng của đồ thị hàm số trên là x = 1.
Tiệm cận ngang của đồ thị hàm số trên là y = -1.
c)
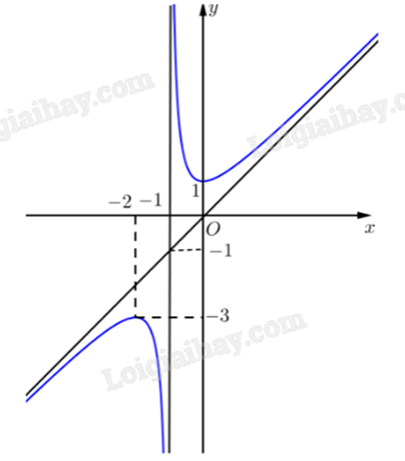
Tiệm cận đứng của đồ thị hàm số trên là x = -1.
Phương trình đường tiệm cận xiên có dạng y = ax + b \((a \ne 0)\).
Đường tiệm cận xiên đi qua hai điểm có toạ độ (0;0) và (-1;-1) nên ta có:
\(\left\{ {\begin{array}{*{20}{l}}{0 = a.0 + b}\\{ - 1 = a.( - 1) + b}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 0}\end{array}} \right. \Rightarrow y = x\)
Vậy phương trình đường tiệm cận xiên là y = x.
5. Bài tập vận dụng
Các bài khác cùng chuyên mục







