Đề thi vào 10 môn Toán Vĩnh Long năm 2018
Tải vềBài 1 (2.0 điểm): a) Tính giá trị biểu thức:
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Bài 1 (2.0 điểm):
a) Tính giá trị biểu thức: \(A = 3\sqrt {27} - 2\sqrt {12} + 4\sqrt {48} .\) b) Rút gọn biểu thức: \(B = \sqrt {7 - 4\sqrt 3 } + \frac{1}{{2 - \sqrt 3 }}.\)
Bài 2 (2.0 điểm): Giải các phương trình và hệ phương trình sau:
a) \({x^2} - 3x + 2 = 0\) b) \({x^2} - 2\sqrt 3 x + 3 = 0\)
c) \({x^4} - 9{x^2} = 0\) d) \(\left\{ \begin{array}{l}x - y = 3\\3x - 2y = 8\end{array} \right.\)
Bài 3 (1.0 điểm):
a) Trong mặt phẳng tọa độ Oxy, cho Parabol (P): \(y = {x^2}\) . Vẽ đồ thị Parabol (P).
b) Cho phương trình: \({x^2} - \left( {m - 1} \right)x - m = 0\,\,\,\left( 1 \right)\) ( với x là ẩn số, m là tham số). Xác định các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn điều kiện: \({x_1}\left( {3 - {x_2}} \right) + 20 \ge 3\left( {3 - {x_2}} \right)\)
Bài 4 (1.0 điểm):
Quãng đường AB dài 160 km. Hai xe khởi hành cùng một lúc từ A để đi đến B. Vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút. Tính vận tốc của xe thứ hai.
Bài 5 (1.0 điểm):
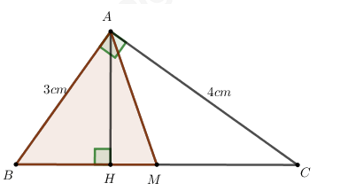
Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của BC. Biết AB = 3 cm, AC = 4cm. Tính độ dài đường cao AH và diện tích tam giác ABM.
Bài 6 (2.5 điểm):
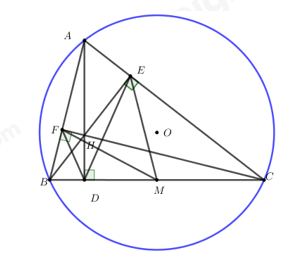
Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Gọi M là trung điểm của BC.
a) Chứng minh tứ giác BFHD nội tiếp được đường tròn.
b) Biết \(\widehat {EBC} = {30^0}.\) Tính số đo \(\widehat {EMC}\) .
c) Chứng minh \(\widehat {FDE} = \widehat {FME}\)
Bài 7 (0.5 điểm): Cho \(a = \frac{{\sqrt 2 - 1}}{2};b = \frac{{\sqrt 2 + 1}}{2}.\) Tính \({a^7} + {b^7}\)
Tìm giá trị nhỏ nhất của biểu thức \(A = 2{x^2} - {y^2} + x + \frac{1}{x} + 1.\)
Lời giải
Bài 1:
Phương pháp:
+) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \;\;\;khi\;\;\;A \ge 0\\ - A\sqrt B \;\;\;khi\;\;\;A < 0\end{array} \right.\) và công thức trục căn thức ở mẫu: \(\frac{1}{{A - \sqrt B }} = \frac{{1 + \sqrt B }}{{{A^2} - B}}.\)
Cách giải:
a) Tính giá trị biểu thức: \(A = 3\sqrt {27} - 2\sqrt {12} + 4\sqrt {48} .\)
\(\begin{array}{l}A = 3\sqrt {27} - 2\sqrt {12} + 4\sqrt {48} \\\;\;\; = 3\sqrt {{3^2}.3} - 2\sqrt {{2^2}.3} + 4.\sqrt {{4^2}.3} \\\;\;\; = 9\sqrt 3 - 4\sqrt 3 + 16\sqrt 3 \\\;\;\; = 21\sqrt 3 .\end{array}\)
Vậy \(A = 21\sqrt 3 .\)
b) Rút gọn biểu thức: \(B = \sqrt {7 - 4\sqrt 3 } + \frac{1}{{2 - \sqrt 3 }}.\)
\(\begin{array}{l}B = \sqrt {7 - 4\sqrt 3 } + \frac{1}{{2 - \sqrt 3 }} = \sqrt {{2^2} - 2.2\sqrt 3 + {{\left( {\sqrt 3 } \right)}^2}} + \frac{{2 + \sqrt 3 }}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}}\\\;\;\; = \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} + 2 + \sqrt 3 = 2 - \sqrt 3 + 2 + \sqrt 3 = 4.\;\;\;\left( {do\;\;2 - \sqrt 3 > 0} \right)\end{array}\)
Vậy B = 4.
Bài 2:
Phương pháp:
a) Sử dụng công thức tìm nghiệm nhanh của phương trình bậc hai: \(a + b + c = 0\) thì phương trình luôn có 1 nghiệm là \(x = 1\) và nghiệm còn lại là: \(x = \frac{c}{a}\) .
b) Sử dụng hằng đẳng thức \({\left( {a - b} \right)^2}\) để tìm nghiệm của phương trình.
c) Cách 1:Đặt \({x^2} = t\left( {t \ge 0} \right)\) Sau đó giải phương trình bậc hai ẩn t để tìm nghiệm.
Cách 2: Đặt \({x^2}\) làm nhân tử chung, đưa phương trình về dạng phương trình tích để tìm x.
d) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
Cách giải:
\(a)\;\;{x^2} - 3x + 2 = 0\)
Ta có: \(a + b + c = 1 - 3 + 2 = 0\) nên phương trình đã cho luôn có hai nghiệm phân biệt là: \({x_1} = 1;{x_2} = \frac{c}{a} = 2\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {1;2} \right\}\) .
\(\begin{array}{l}b)\;\;{x^2} - 2\sqrt 3 x + 3 = 0\\ \Leftrightarrow {\left( {x - \sqrt 3 } \right)^2} = 0\\ \Leftrightarrow x = \sqrt 3 .\end{array}\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ {\sqrt 3 } \right\}\)
\(c)\;\;{x^4} - 9{x^2} = 0 \Leftrightarrow {x^2}\left( {{x^2} - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 3\\x = 3\end{array} \right..\)
Vậy tập nghiệm của phương trình là: \(S = \left\{ { - 3;0;3} \right\}\)
\(d)\;\;\left\{ \begin{array}{l}x - y = 3\\3x - 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 3y = 9\\3x - 2y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 1\\x = 3 + y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - 1\\x = 2\end{array} \right.\)
Vậy hệ phương trình đã cho có một nghiệm duy nhất: \(\left( {x;y} \right) = \left( {2; - 1} \right)\)
Bài 3:
Phương pháp:
a) Lập bảng giá trị x, y tương ứng với các điểm mà đồ thị (P) đi qua.
b) Bước 1: Tìm m để phương trình có 2 nghiệm phân biệt: PT có 2 nghiệm phân biệt \(\left( {\Delta \left( {\Delta '} \right) > 0} \right)\)
Bước 2: Kết hợp hệ thức Vi-et với điều kiện đề bài để tìm m. Hệ thức Vi-et: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\)
Cách giải:
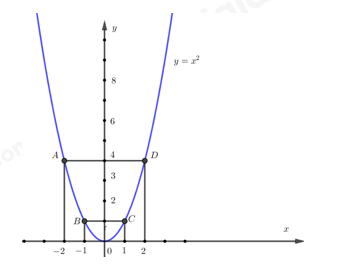
a) Trong mặt phẳng tọa độ Oxy, cho Parabol (P): \(y = {x^2}\) . Vẽ đồ thị Parabol (P).
Bảng giá trị
|
x |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Khi đó đồ thị hàm số đã cho là 1 đường cong và đi qua các điểm \(A\left( { - 2;4} \right);B\left( { - 1;1} \right);C\left( {1;1} \right);D\left( {2;4} \right);O\left( {0;0} \right)\)
b) Cho phương trình: \({x^2} - \left( {m - 1} \right)x - m = 0\,\,\,\left( 1 \right)\) (với x là ẩn số, m là tham số). Xác định các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn điều kiện: \({x_1}\left( {3 - {x_2}} \right) + 20 \ge 3\left( {3 - {x_2}} \right)\)
+) Phương trình có hai nghiệm phân biệt
\(\begin{array}{l} \Leftrightarrow \Delta > 0 \Leftrightarrow {\left( {m - 1} \right)^2} + 4m > 0\\ \Leftrightarrow {m^2} + 2m + 1 > 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} > 0\\ \Leftrightarrow m \ne - 1\end{array}\)
+) Áp dụng hệ thức Vi-et cho phương trình (1) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 1\\{x_1}.{x_2} = - m\end{array} \right.\)
Theo đầu bài ta có
\(\begin{array}{l}{x_1}\left( {3 - {x_2}} \right) + 20 \ge 3\left( {3 - {x_2}} \right)\\ \Leftrightarrow 3{x_1} - {x_1}{x_2} + 20 \ge 9 - 3{x_2}\\ \Leftrightarrow 3\left( {{x_1} + {x_2}} \right) - {x_1}{x_2} + 11 \ge 0\\ \Leftrightarrow 3.\left( {m - 1} \right) + m + 11 \ge 0\\ \Leftrightarrow 4m + 8 \ge 0\\ \Leftrightarrow m \ge - 2\end{array}\)
Kết hợp với điều kiện \(m \ne - 1\) ta có: \(m \ge - 2;m \ne - 1\) thỏa mãn yêu cầu bài toán.
Bài 4:
Phương pháp:
Các bước giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
+) Đặt ẩn và tìm điều kiện cho ẩn
+) Biểu thị các đại lượng chưa biết qua ẩn
+) Lập phương trình hoặc hệ phương trình theo ẩn
+) Giải phương trình và đối chiếu với điều kiện của ẩn sau đó kết luận
Cách giải:
Quãng đường AB dài 160 km. Hai xe khởi hành cùng một lúc từ A để đi đến B. Vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút. Tính vận tốc của xe thứ hai.
Gọi vận tốc của xe thứ hai là \(x\left( {km/h} \right),\,\,\left( {x > 0} \right)\)
Vận tốc của xe thứ nhất là: \(x + 10\left( {km/h} \right)\)
Thời gian xe thứ nhất đi hết quãng đường AB là:: \(\frac{{160}}{{x + 10}}\left( h \right)\)
Thời gian xe thứ hai đi hết quãng đường AB là: \(\frac{{160}}{x}\,\,\left( h \right)\)
Ta có xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút: \( = \frac{{48}}{{60}} = \frac{4}{5}\,\,\left( h \right)\)
Theo bài ra ta có phương trình:
\(\begin{array}{l}\;\;\;\;\;\frac{{160}}{x} - \frac{{160}}{{x + 10}} = \frac{4}{5}\\ \Leftrightarrow 160.5.\left( {x + 10} \right) - 160.5.x = 4x\left( {x + 10} \right)\\ \Leftrightarrow 800x + 8000 - 800x = 4{x^2} + 40x\\ \Leftrightarrow {x^2} + 10x - 2000 = 0\\ \Leftrightarrow \left( {x - 40} \right)\left( {x + 50} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 40 = 0\\x + 50 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 40\left( {tm} \right)\\x = - 50\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy xe thứ hai đi với vận tốc là: 40km/h.
Bài 5:
Phương pháp:
Áp dụng hệ thức đường cao trong tam giác vuông
để tính AH.
Áp dụng định lý Pytago trong tam giác vuông ABC để tính BC.
Sử dụng công thức tính diện tích tam giác ABM:
\({S_{ABM}} = \frac{1}{2}AH.BM\)
Cách giải:
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} = \frac{{25}}{{144}} \Rightarrow AH = 2,4cm\)
Áp dụng định lý Pytago trong tam giác vuông ABC có
\(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25 \Rightarrow BC = 5\left( {cm} \right)\)
Do M là trung điểm của BC nên ta có: \(BM = \frac{1}{2}BC = \frac{5}{2} = 2,5\left( {cm} \right)\)
Xét tam giác ABM có đường cao AH ta có: \({S_{ABM}} = \frac{1}{2}AH.BM = \frac{1}{2}.2,4.2,5 = 3\left( {c{m^2}} \right)\)
Bài 6:
Cách giải:
a) Chứng minh tứ giác BFHD nội tiếp được đường tròn.
Ta có: AD, CF lần lượt là các đường cao của tam giác ABC nên: \(\widehat {ADB} = \widehat {BFC} = {90^0}\,\,\left( {hay\,\,\,\widehat {HDB} = \widehat {BFH} = {{90}^0}\,\,} \right)\)
Nên: \(\widehat {BFH} + \widehat {BDH} = {180^0}\)
Suy ra tứ giác BFHD nội tiếp được đường tròn đường kính BH với tâm là trung điểm của BH. (tổng 2 góc đối trong 1 tứ giác bằng \({180^0}\)
b) Biết \(\widehat {EBC} = {30^0}.\) Tính số đo \(\widehat {EMC}\) .
Ta có: \(\widehat {EBC} = {30^0} \Rightarrow \widehat {BCE} = {90^0} - {30^0} = {60^0}\,\,\left( {BE \bot EC\,} \right)\)
Xét tam giác vuông BEC vuông tại E có EM là trung tuyến nên: \(EM = MC = MB = \frac{1}{2}BC\)
Nên tam giác EMC là tam giác đều khi đó ta có: \(\widehat {EMC} = {60^0}\)
Vậy \(\widehat {EMC} = {60^0}\)
c) Chứng minh \(\widehat {FDE} = \widehat {FME}\)
Xét tứ giác BFEC ta có: \(\widehat {BFC} = \widehat {BEC} = {90^0}\left( {gt} \right)\)
Mà 2 đỉnh E, F kề nhau cùng nhìn cạnh BC dưới 1 góc vuông nên tứ giác BFEC nội tiếp.
\( \Rightarrow \widehat {EFC} = \widehat {EBC}\left( {\,hay\,\,\widehat {EFH} = \widehat {HBD}} \right)\) (2 góc nội tiếp cùng chắn cung EC) (1)
Mà tứ giác BFHD nội tiếp đường tròn (chứng minh câu a)
\( \Rightarrow \widehat {HBD} = \widehat {HFD}\) (2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) ta có: \(\widehat {EFH} = \widehat {HFD}\).
Mà \(\widehat {EFH} = \widehat {HAE}\) (tứ giác AFHE nội tiếp)
\(\widehat {HFD} = \widehat {HBD}\) (tứ giác BFHD nội tiếp)
Từ đó ta có: \(\widehat {DFE} = \widehat {DFH} + \widehat {HFE} = 2\widehat {HAE} = 2\left( {{{90}^0} - \widehat {MEC}} \right) = {180^0} - 2\widehat {MEC} = \widehat {EMC}\) (do tam giác MEC cân tại M)
Xét tứ giác DFEM ta có: \(\widehat {DFE} = \widehat {EMC}\) nên tứ giác DFEM nội tiếp.
Vậy ta có: \(\widehat {FDE} = \widehat {FME}\)
Bài 7:
Cách giải:
Ta có:
\(\begin{array}{l}a + b = \frac{{\sqrt 2 - 1}}{2} + \frac{{\sqrt 2 + 1}}{2} = \sqrt 2 \\a.b = \frac{{\sqrt 2 - 1}}{2}.\frac{{\sqrt 2 + 1}}{2} = \frac{1}{4}\end{array}\)
\({a^2} + {b^2} = {\left( {a + b} \right)^2} - 2ab = {\left( {\sqrt 2 } \right)^2} - 2.\frac{1}{4} = \frac{3}{2}\)
\({a^4} + {b^4} = {\left( {{a^2} + {b^2}} \right)^2} - 2{a^2}{b^2} = {\left( {\frac{3}{2}} \right)^2} - 2.{\left( {\frac{1}{4}} \right)^2} = \frac{{17}}{8}\)
\({a^3} + {b^3} = {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right) = {\left( {\sqrt 2 } \right)^3} - 3\frac{1}{4}.\sqrt 2 = \frac{{5\sqrt 2 }}{4}\)
Do đó: \({a^7} + {b^7} = \left( {{a^3} + {b^3}} \right)\left( {{a^4} + {b^4}} \right) - {a^3}{b^3}\left( {a + b} \right) = \frac{{5\sqrt 2 }}{4}.\frac{{17}}{8} - {\left( {\frac{1}{4}} \right)^3}.\sqrt 2 = \frac{{169\sqrt 2 }}{{64}}\)