Đề thi vào 10 môn Toán Trà Vinh năm 2023
Tải vềCâu 1: a) Tính giá trị biểu thức \(A = \sqrt {20} - 2\sqrt {80} + 3\sqrt {45} \). b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 12\\x - 2y = - 4\end{array} \right.\) c) Giải phương trình \({x^4} - {x^2} - 12 = 0\).
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Câu 1:
a) Tính giá trị biểu thức \(A = \sqrt {20} - 2\sqrt {80} + 3\sqrt {45} \).
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 12\\x - 2y = - 4\end{array} \right.\)
c) Giải phương trình \({x^4} - {x^2} - 12 = 0\).
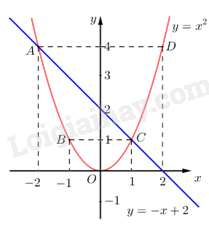
Câu 2: Trong mặt phẳng toạ đô Oxy, cho \(\left( P \right):y = {x^2}\)và đường thẳng \(\left( d \right):y = - x + 2.\)
a) Vẽ đồ thị hai hàm số \((P)\) và \((d)\).
b) Bằng phép toán, tìm tọa độ giao điểm của \((P)\) và \((d)\).
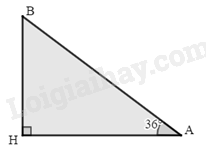
Câu 3: Thang cuốn ở siêu thị giúp khách hàng di chuyển từ tầng này sang tầng khác tiện lợi. Biết rằng thang cuốn được thiết kế có độ nghiêng so với mặt phẳng ngang là \(36^\circ \left( {\widehat {BAH} = 36^\circ } \right)\) và có vận tốc là 0,5m/s. Một khách hàng đã di chuyển bằng thang cuốn từ tầng một lên tầng hai theo hướng AB hết 12 giây. Tính chiều cao \((BH)\) của thang cuốn? (Kết quả làm tròn đến chữ số thập phân thứ nhất).
Câu 4: Từ điểm M nằm bên ngoài đường tròn tâm O, vẽ hai tiếp tuyến MA và MB với đường tròn (A, B là tiếp điểm).
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Vẽ đường kính AC của (O), gọi D là giao điểm của MC và (O), biết D khác C. Chứng minh \(M{A^2} = MD.{\rm{ }}MC\)
c) Hai đoạn thẳng AB và MO cắt nhau tại H, kẻ đường kính BE của (O). Chứng minh ba điểm E, H, D thẳng hàng.
Câu 5: Cho phương trình \({x^2} + 3x + m + 1 = 0\) ( \(m\) là tham số). (1)
a) Tìm \(m\) để phương trình có hai nghiệm.
b) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình. Tìm giá trị lớn nhất của biểu thức \(P = {\left( {{x_1} - {x_2}} \right)^2} + 7m + 5{x_1}{x_2}\)
--- HẾT---
Lời giải chi tiết
Câu 1 (TH):
Phương pháp:
a) Khai phương căn bậc hai và rút gọn
b) Giải hệ bằng phương pháp thế hoặc cộng đại số
c) Đặt \(t = {x^2}\) và giải phương trình bậc 2.
Cách giải:
a) Tính giá trị biểu thức \(A = \sqrt {20} - 2\sqrt {80} + 3\sqrt {45} \).
Ta có:
\(\begin{array}{l}A = \sqrt {20} - 2\sqrt {80} + 3\sqrt {45} \\A = \sqrt {{2^2}.5} - 2\sqrt {{4^2}.5} + 3\sqrt {{3^2}.5} \\A = 2.\sqrt 5 - 2.4\sqrt 5 + 3.3\sqrt 5 \\A = 2\sqrt 5 - 8\sqrt 5 + 9\sqrt 5 \\A = \left( {2 - 8 + 9} \right).\sqrt 5 \\A = 3\sqrt 5 \end{array}\)
Vậy \(A = 3\sqrt 5 \).
b) Giải hệ phương trình \(\left\{ \begin{array}{l}3x + 2y = 12\\x - 2y = - 4\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}3x + 2y = 12\\x - 2y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 8\\2y = x + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\).
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;3} \right)\).
c) Giải phương trình \({x^4} - {x^2} - 12 = 0\).
Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), phương trình trở thành \({t^2} - t - 6 = 0\).
Ta có \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 6} \right) = 25 > 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{t_1} = \frac{{1 + \sqrt {25} }}{{2.1}} = 3\,\,\,\,\left( {tm} \right)\\{t_2} = \frac{{1 - \sqrt {25} }}{{2.1}} = - 2\,\,\left( {tm} \right)\end{array} \right.\).
Với \(t = 3 \Rightarrow {x^2} = 3 \Leftrightarrow x = \pm \sqrt 3 \).
Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm \sqrt 3 } \right\}\).
Câu 2 (TH):
Phương pháp:
a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ Oxy
b) Xét phương trình hoành độ giao điểm của (d) và (P).
Cách giải:
a) Vẽ đồ thị hai hàm số \((P)\) và \((d)\).
* Vẽ đồ thị hàm số \(\left( d \right):y = - x + 2\)
Lấy \(x = 0 \Rightarrow y = 2\)
\(y = 0 \Rightarrow x = 2\)
\( \Rightarrow \)Đồ thị hàm số \(\left( d \right):y = - x + 2\) là đường thẳng đi qua hai điểm \(\left( {2;0} \right)\) và \(\left( {0;2} \right)\).
* Vẽ đồ thị hàm số \(\left( P \right):y = {x^2}\)
Ta có bảng giá trị sau:
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = {x^2}\) |
4 |
1 |
0 |
1 |
4 |
\( \Rightarrow \) Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\,\left( {0;0} \right);A\left( { - 2;4} \right);\,\,B\left( { - 1;1} \right);C\left( {1;1} \right);\,\,D\left( {2;4} \right)\)
Hệ số \(a = 1 > 0\) nên parabol có bề cong hướng lên. Đồ thị hàm số nhận Oy làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = {x^2}\) như sau:
b) Bằng phép toán, tìm tọa độ giao điểm của \((P)\) và \((d)\).
Xét phương trình hoành độ giao điểm của \((P)\) và \((d)\) ta có:
\(\begin{array}{l}{x^2} = - x + 2\\ \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\end{array}\)
Với \(x = 1\) ta có: \(y = {1^2} = 1\)
Với \(x = - 2\) ta có: \(y = {\left( { - 2} \right)^2} = 4\)
Vậy \((P)\)cắt \((d)\) tại \(\left( { - 2;4} \right)\) và \(\left( {1;1} \right)\).
Câu 3 (TH):
Phương pháp:
Áp dụng tỉ số lượng giác của góc nhọn.
Cách giải:
Chiều dài thang máy là: \(12.0,5 = 6\left( m \right)\)
Trong DAHB vuông tại H ta có \(\sin \widehat {HAB} = \frac{{HB}}{{AB}}\)
Chiều cao HB của thang cuốn là: \(HB = \sin \widehat {HAB}.AB = \sin {36^0}.6 \approx 3,5\left( m \right)\)
Vậy chiều cao thang cuốn là 3,5m.
Câu 4 (VD):
Phương pháp:
a) Tổng hai góc đối diện bằng \({180^0}\)
b) Chứng minh $\Delta MAD\backsim \Delta MCA\left( g.g \right)$
c) Chứng minh tổng các góc bằng \({180^0}\).
Cách giải:
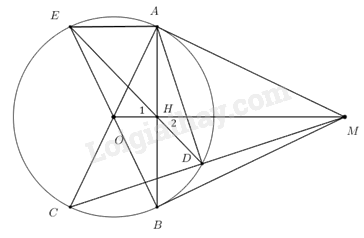
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
Do MA, MB là tiếp tuyến của (O) nên \(MA \bot OA,MB \bot OB\) (tính chất)
\(\begin{array}{l} \Rightarrow \angle MAO = \angle MBO = {90^0}\\ \Rightarrow \angle MAO + \angle MBO = {90^0} + {90^0} = {180^0}\end{array}\)
Mà hai góc này ở vị trí đối diện của tứ giác MAOB nên tứ giác MAOB nội tiếp (dhnb) (đpcm)
b) Vẽ đường kính AC của (O), gọi D là giao điểm của MC và (O), biết D khác C. Chứng minh \(M{A^2} = MD.{\rm{ }}MC\)
Xét \(\Delta MAD\) và \(\Delta MCA\) có:
\(\angle AMC\) chung
\(\angle MAD = \angle MCA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung)
$\Rightarrow \Delta MAD\backsim \Delta MCA\left( g.g \right)\Rightarrow \frac{MA}{MC}=\frac{MD}{MA}\Leftrightarrow M{{A}^{2}}=MC.MD$ (đpcm)
c) Hai đoạn thẳng AB và MO cắt nhau tại H, kẻ đường kính BE của (O). Chứng minh ba điểm E, H, D thẳng hàng.
Do MA, MB là 2 tiếp tuyến cắt nhau của (O) nên MA = MB (tính chất)
Mà OA = OB (bằng bán kính) nên MO là trung trực của AB (tính chất)
\( \Rightarrow \) \(MO \bot AB\) tại H và H là trung điểm của AB
Khi đó xét tam giác MAO vuông tại A, đường cao AH có \(M{A^2} = MH.MO\) (hệ thức lượng trong tam giác vuông)
Mà \(M{A^2} = MC.MD\) (cmt) nên suy ra \(MH.MO = MD.MC \Leftrightarrow \frac{{MH}}{{MC}} = \frac{{MD}}{{MO}}\)
Xét \(\Delta MHD\) và \(\Delta MCO\) có
\(\angle OMC\) chung
\(\frac{{MH}}{{MC}} = \frac{{MD}}{{MO}}\)
$\Rightarrow \Delta MHD\backsim \Delta MCO\left( c.g.c \right)\Rightarrow \angle {{H}_{2}}=\angle MCO$ (2 góc tương ứng) (1)
Do BE đường kính nên \(\angle BAE = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow AE \bot AB\) mà \(AO \bot AB \Rightarrow AE\parallel AO\)
\( \Rightarrow \angle {H_1} = \angle AED\) (so le trong) (2)
Mà \(\angle AED = \angle ACD\) (góc nội tiếp cùng chắn cung AD) (3)
Từ (1) (2) (3) suy ra \(\angle {H_1} = \angle {H_2}\)
Mà \(\angle {H_1} + \angle EHM = {180^0}\) (2 góc kề bù) \( \Rightarrow {H_2} + \angle MHE = {180^0}\)
\( \Rightarrow E,H,D\) thẳng hàng
Câu 5 (VD):
Phương pháp:
a) Tính \(\Delta \) và cho \(\Delta \ge 0\)
b) Áp dụng hệ thức Viet
Cách giải:
a) Tìm \(m\) để phương trình có hai nghiệm.
Do \(a = 1 \ne 0\) nên phương trình (1) là phương trình bậc 2
Ta có \(\Delta = {3^2} - 4.1\left( {m + 1} \right) = 9 - 4m - 4 = 5 - 4m\)
Để phương trình có 2 nghiệm thì \(\Delta \ge 0 \Leftrightarrow 5 - 4m \ge 0 \Leftrightarrow m \le \frac{5}{4}\)
Vậy \(m \le \frac{5}{4}\) thì phương trình (1) có 2 nghiệm.
b) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình. Tìm giá trị lớn nhất của biểu thức \(P = {\left( {{x_1} - {x_2}} \right)^2} + 7m + 5{x_1}{x_2}\)
Theo a, với \(m \le \frac{5}{4}\) thì phương trình (1) có 2 nghiệm \({x_1},{x_2}\)
Áp dụng hệ thức Viet ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 3\\{x_1}.{x_2} = m + 1\end{array} \right.\)
Ta có \(P = {\left( {{x_1} - {x_2}} \right)^2} + 7m + 5{x_1}{x_2}\)
\(\begin{array}{l} = x_1^2 + x_2^2 - 2{x_1}{x_2} + 7m + 5{x_1}{x_2}\\ = x_1^2 + 2{x_1}{x_2} + x_2^2 + 7m + {x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} + {x_1}{x_2} + 7m\\ = {\left( { - 3} \right)^2} + m + 1 + 7m\\ = 8m + 10\end{array}\)
\( \Rightarrow P = 8m + 10\)
Với \(m \le \frac{5}{4}\)\( \Rightarrow 8m \le 10 \Rightarrow 8m + 10 \le 20 \Leftrightarrow P \le 20\)
Vậy GTLN của \(P = 20\) khi \(m = \frac{5}{4}\).












