Đề thi vào 10 môn Toán Tây Ninh năm 2021
Tải vềCâu 1 (1 điểm): Rút gọn biểu thức:
Đề bài
Câu 1 (1 điểm): Rút gọn biểu thức: \(P = 3\sqrt 4 + 2\sqrt {25} - \sqrt {16} .\)
Câu 2 (1 điểm): Giải phương trình: \({x^2} - 7x + 12 = 0\).
Câu 3 (1 điểm): Tìm \(x\) để biểu thức \(T = \dfrac{{{x^2} + 1}}{{3x - 2}}\) xác định.
Câu 4 (1 điểm): Vẽ đồ thị hàm số \(y = 2{x^2}.\)
Câu 5 (1 điểm): Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 3,\,\,AC = 2.\) Trên cạnh \(AB\) lấy điểm \(M\) sao cho \(BM = 2.\) Tính độ dài đoạn thẳng \(CM.\)
Câu 6 (1 điểm): Cho hệ phương trình \(\left\{ \begin{array}{l}ax - 2y = b\\2x - by = - 2a\end{array} \right..\) Tìm \(a\) và \(b\) biết hệ phương trình đã cho có nghiệm là \(\left( {2;\,\, - 1} \right).\)
Câu 7 (1 điểm): Tìm \(m\) để phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 3m + 2 = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - 3{x_1}{x_2} = 0.\)
Câu 8 (1 điểm): Một đoàn khách du lịch gồm 40 người dự định tham quan đỉnh núi Bà Đen, nóc nhà Đông Nam Bộ bằng cáp treo khứ hồi (gồm lượt lên và lượt xuống). Nhưng khi tới nơi có 5 bạn trẻ muốn khám phá bằng đường bộ khi leo lên còn lúc xuống sẽ đi cáp treo để trải nghiệm nên 5 bạn chỉ mua vé lượt xuống, do đó đoàn đã chi ra 9.450.000 đồng để mua vé. Hỏi giá cáp treo khứ hồi và giá vé 1 lượt là bao nhiêu? Biết rằng giá vé 1 lượt rẻ hơn giá vé khứ hối là 110.000 đồng.
Câu 9 (1 điểm): Cho \(\Delta ABC\) vuông tại \(A\) ngoại tiếp đường tròn \(\left( O \right).\) Gọi \(D,\,\,E,\,\,F\) lần lượt là các tiếp điểm của \(\left( O \right)\) với các cạnh \(AB,\,\,AC\) và \(BC.\) Đường thẳng \(BO\) cắt đường thẳng \(EF\) tại \(I.\) Tính \(\angle BIF.\)
Câu 10 (1 điểm): Cho hình chữ nhật \(ABCD.\) Gọi \(M,\,\,N\) lần lượt là trung điểm của các cạnh \(BC\) và \(CD.\) Gọi \(E\) là giao điểm của \(BN\) với \(AM\) và \(F\) là giao điểm của \(BN\) với \(DM;\,\,DM\) cắt \(AN\) tại\(K.\) Chứng minh điểm \(A\) nằm trên đường tròn ngoại tiếp tam giác \(EFK.\)
Lời giải
Câu 1 (TH):
Phương pháp:
Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
Cách giải:
\(\begin{array}{l}P = 3\sqrt 4 + 2\sqrt {25} - \sqrt {16} \\\,\,\,\,\, = 3\sqrt {{2^2}} + 2\sqrt {{5^2}} - \sqrt {{4^2}} \\\,\,\,\,\, = 3.2 + 2.5 - 4\\\,\,\,\,\, = 6 + 10 - 4\\\,\,\,\,\, = 12.\end{array}\)
Vậy \(P = 12.\)
Câu 2 (TH):
Phương pháp:
Tính \(\Delta = {b^2} - 4ac\) (hoặc \(\Delta ' = {\left( {b'} \right)^2} - ac\)), sử dụng công thức nghiệm của phương trình bậc hai một ẩn: \({x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta }}{{2a}}\) (hoặc \({x_{1,2}} = \dfrac{{ - b' \pm \sqrt {\Delta '} }}{a}\)), tính được nghiệm của phương trình, kết luận.
Cách giải:
\({x^2} - 7x + 12 = 0\)
Phương trình có:\(\Delta = {7^2} - 4.12 = 49 - 48 = 1 > 0\)
\( \Rightarrow \) Phương trình đã cho có 2 nghiệm phân biệt \({x_1} = \dfrac{{7 + \sqrt 1 }}{2} = 4\) và \({x_2} = \dfrac{{7 - \sqrt 1 }}{2} = 3.\)
Vậy phương trình đã cho có tập nghiệm: \(S = \left\{ {3;\,\,4} \right\}.\)
Câu 3 (TH):
Phương pháp:
\(\dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) xác định \( \Leftrightarrow g\left( x \right) \ne 0\)
Cách giải:
Biểu thức \(T = \dfrac{{{x^2} + 1}}{{3x - 2}}\) xác định \( \Leftrightarrow 3x - 2 \ne 0\)\( \Leftrightarrow x \ne \dfrac{2}{3}.\)
Vậy \(x \ne \dfrac{2}{3}\) thì biểu thức đã cho xác định.
Câu 4 (TH):
Phương pháp:
Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
Cách giải:
Ta có bảng giá trị:
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y\) |
\(8\) |
\(2\) |
\(0\) |
\(2\) |
\(8\) |
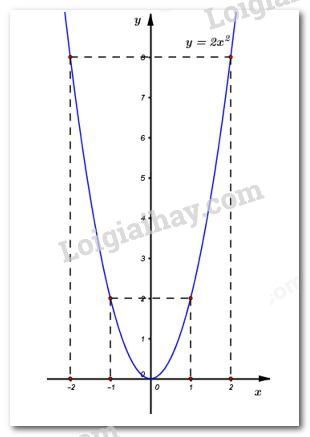
Vậy đồ thị hàm số \(y = 2{x^2}\) là đường cong đi qua các điểm: \(\left( { - 2;\,\,8} \right),\,\,\left( { - 1;\,\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,2} \right)\) và \(\left( {2;\,\,8} \right).\)
Câu 5 (VD):
Phương pháp:
Tính \(AM\)
Áp dụng định lý Py – ta – go cho \(\Delta ACM\) vuông tại \(A\), tính \(CM\)
Cách giải:
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 3,\,\,AC = 2.\) Trên cạnh \(AB\) lấy điểm \(M\) sao cho \(BM = 2.\) Tính độ dài đoạn thẳng \(CM.\)
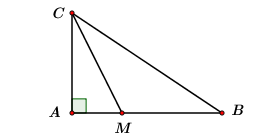
Theo đề bài ta có: \(MB = 2\) và \(M \in AB\)
\( \Rightarrow AM = AB - MB = 3 - 2 = 1.\)
Áp dụng định lý Py – ta - go cho \(\Delta ACM\) vuông tại \(A\) ta có:
\(CM = \sqrt {A{M^2} + A{C^2}} \)\( = \sqrt {{1^2} + {2^2}} = \sqrt 5 .\)
Vậy \(CM = \sqrt 5 .\)
Câu 6 (VD):
Phương pháp:
Vì \(\left( {2;\, - 1} \right)\) là nghiệm của hệ phương trình, thay vào hệ ban đầu ta được hệ phương trình mới có ẩn là \(a,b\)
Sử dụng phương pháp cộng đại số, tìm được nghiệm \(a\)
Sử dụng phương pháp thế, tìm được nghiệm \(b\)
Tìm được \(a,b\) thỏa mãn bài toán.
Cách giải:
Ta có: \(\left( {2;\, - 1} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}ax - 2y = b\\2x - by = - 2a\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a.2 - 2.\left( { - 1} \right) = b\\2.2 - b.\left( { - 1} \right) = - 2a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a + 2 = b\\4 + b = - 2a\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2a - b = - 2\\2a + b = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a = - 6\\b = 2a + 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{3}{2}\\b = 2.\left( { - \dfrac{3}{2}} \right) + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{3}{2}\\b = - 1\end{array} \right.\end{array}\)
Vậy \(a = - \dfrac{3}{2}\) và \(b = - 1\) thỏa mãn bài toán.
Câu 7 (VD):
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt \(\Delta > 0\) (hoặc \(\Delta ' > 0\))
Áp dụng hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\) theo \(m\)
Thay vào \(x_1^2 + x_2^2 - 3{x_1}{x_2} = 0\), tìm được \(m\), đối chiếu điều kiện và kết luận.
Cách giải:
Xét phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 3m + 2 = 0\,\,\,\,\left( * \right)\)
Phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\)\( \Leftrightarrow \Delta ' > 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {m - 1} \right)^2} - \left( {{m^2} - 3m + 2} \right) > 0\\ \Leftrightarrow {m^2} - 2m + 1 - {m^2} + 3m - 2 > 0\\ \Leftrightarrow m - 1 > 0\\ \Leftrightarrow m > 1\end{array}\)
Với \(m > 1\) thì phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)
Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right)\\{x_1}{x_2} = {m^2} - 3m + 2\end{array} \right..\)
Theo đề bài ta có: \(x_1^2 + x_2^2 - 3{x_1}{x_2} = 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 3{x_1}{x_2} = 0\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2} = 0\\ \Leftrightarrow 4{\left( {m - 1} \right)^2} - 5\left( {{m^2} - 3m + 2} \right) = 0\\ \Leftrightarrow 4{m^2} - 8m + 4 - 5{m^2} + 15m - 10 = 0\\ \Leftrightarrow - {m^2} + 7m - 6 = 0\\ \Leftrightarrow {m^2} - 7m + 6 = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\,\,\,\left( {ktm} \right)\\m = 6\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(m = 6\) thỏa mãn bài toán.
Câu 8 (VD):
Phương pháp:
Gọi giá vé cáp treo khứ hồi và giá vé cáp treo 1 lượt lần lượt là \(x\) và \(y\) (đồng), \(\left( {x > y > 0,\,\,\,x > 110.000} \right).\)
Vì giá vé cáp treo 1 lượt rẻ hơn giá vé cáp treo khứ hồi là \(110.000\) ta lập được phương trình (1)
Dựa vào số người mua vé cáp treo khứ hỏi và số người mua vé cáo treo một lượt ta lập được phương trình (2)
Từ (1) và (2), lập được hệ phương trình, giải hệ phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Gọi giá vé cáp treo khứ hồi và giá vé cáp treo 1 lượt lần lượt là \(x\) và \(y\) (đồng), \(\left( {x > y > 0,\,\,\,x > 110.000} \right).\)
Vì giá vé cáp treo 1 lượt rẻ hơn giá vé cáp treo khứ hồi là \(110.000\) đồng nên ta có phương trình: \(x - y = 110.000\,\,\,\left( 1 \right)\)
Có \(40 - 5 = 35\) người mua vé cáp treo khứ hồi và \(5\) người mua vé cáp treo 1 lượt nên ta có phương trình:
\(35x + 5y = 9.450.000\,\)\( \Leftrightarrow 7x + y = 1.890.000\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}x - y = 110.000\\7x + y = 1.890.000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8x = 2.000.000\\y = x - 110.000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 250.000\,\,\,\left( {tm} \right)\\y = 250.000 - 110.000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 250.000\\y = 140.000\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy giá vé cáp treo khứ hồi là 250.000 đồng và giá vé cáp treo 1 lượt là 140.000 đồng.
Câu 9 (VD):
Phương pháp:
Ta sẽ chứng minh:
+ \(DEIO\) là tứ giác nội tiếp \( \Rightarrow \angle BIF = \angle ODE\)
+ \(ODAE\) là hình vuông \( \Rightarrow \angle ODE = {45^0}\)
Cách giải:
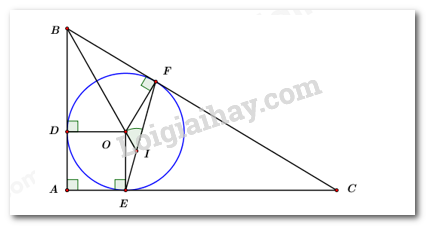
Ta có: \(\angle DEI = \angle DEF = \dfrac{1}{2}\angle DOF\) (góc nội tiếp và góc ở tâm cùng chắn cung \(DF\)).
Vì \(BD,\,\,BF\) là các tiếp tuyến của \(\left( O \right)\) lần lượt tại \(D,\,\,F\) nên \(OB\) là tia phân giác của \(\angle DOF\) (tính chất 2 tiếp tuyến cắt nhau).
\( \Rightarrow \angle DOB = \dfrac{1}{2}\angle DOF\).
\( \Rightarrow \angle DEI = \angle DOB\).
\( \Rightarrow DEIO\) là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện).
Xét tứ giác \(ODAE\) có \(\angle ODA = \angle DAE = \angle OEA = {90^0}\) nên \(ODAE\) là hình chữ nhật (tứ giác có 3 góc vuông).
Lại có \(AD,\,\,AE\) là các tiếp tuyến của \(\left( O \right)\) tại \(D,\,\,E\) nên \(AD = AE\) (tính chất 2 tiếp tuyến cắt nhau)
\( \Rightarrow ODAE\) là hình vuông (hình chữ nhật có 2 cạnh kề bằng nhau) \( \Rightarrow \angle ODE = {45^0}\).
Mà \(DEIO\) là tứ giác nội tiếp (cmt).
\( \Rightarrow \angle BIF = \angle ODE = {45^0}\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Vậy \(\angle BIF = {45^0}\).
Câu 10 (VDC):
Phương pháp:
+ Ta sẽ chứng minh: \(\angle MAN = {90^0} - \angle NAD - \angle MDC\,\,\,\,\left( 1 \right)\) và \(\angle DFN = {90^0} - \angle DAN - \angle FDN\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\angle MAN = \angle DFN\)
+ Vận dụng dấu hiệu nhận biết: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
\( \Rightarrow A\) là điểm nằm trên đường tròn ngoại tiếp \(\Delta EFK.\)
Cách giải:
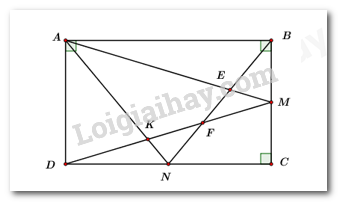
Xét \(\Delta ABM\) và \(\Delta DCM\) ta có:
\(\begin{array}{l}\angle B = \angle C = {90^0}\\BM = MC\,\,\left( {gt} \right)\\DC = AB\,\,\left( {gt} \right)\\ \Rightarrow \Delta ABM = \Delta DCM\,\,\left( {2cgv} \right).\end{array}\)
\( \Rightarrow \angle BAM = \angle MDC\) (hai góc tương ứng bằng nhau)
Hay \(\angle MAB = \angle MDC.\)
Ta có: \(\angle MAN = {90^0} - \angle NAD - \angle MAB\) \( \Rightarrow \angle MAN = {90^0} - \angle NAD - \angle MDC\,\,\,\,\left( 1 \right)\)
Lại có: \(\angle DFN = \angle FNC - \angle FDN\) (góc ngoài của \(\Delta DN\))
Xét \(\Delta AND\) và \(\Delta BNC\) ta có:
\(\begin{array}{l}\angle D = \angle C = {90^0}\\AD = BC\,\,\left( {gt} \right)\\DN = NC\,\,\left( {gt} \right)\\ \Rightarrow \Delta ADN = \Delta BCN\,\,\left( {2cgv} \right)\end{array}\)
\( \Rightarrow \angle BNC = \angle AND\) (hai góc tương ứng)
Hay \(\angle FNC = \angle AND\)
Mà \(\angle AND = {90^0} - \angle DAN\) (hai góc phụ nhau)
\( \Rightarrow \angle DFN = {90^0} - \angle DAN - \angle FDN\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\angle MAN = \angle DFN\)
Mặt khác: \(\angle DFN + \angle KFN = {180^0}\)
\( \Rightarrow \angle KAE + \angle KFE = {180^0}\)
\( \Rightarrow AEFK\) là tứ giác nội tiếp. (dhnb)
\( \Rightarrow A\) là điểm nằm trên đường tròn ngoại tiếp \(\Delta EFK.\) (đpcm)












