Đề thi vào 10 môn Toán Sóc Trăng năm 2021
Tải vềBài 1. Rút gọn biểu thức:
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Phương pháp giải:
Bài 1. Rút gọn biểu thức: \(A = 3\sqrt {48} + \sqrt {75} - 2\sqrt {108} \).
Bài 2. Giải hệ phương trình và phương trình:
a) \(\left\{ \begin{array}{l}2x + 3y = 8\\ - x + y = 1\end{array} \right.\)
b) \({x^4} + 7{x^2} - 18 = 0\).
Bài 3. Cho hàm số \(y = {x^2}\) có đồ thị \(\left( P \right)\).
a) Vẽ đồ thị \(\left( P \right)\) trên mặt phẳng tọa độ \(Oxy\).
b) Tìm giá trị của \(m\) để đường thẳng \(\left( d \right):y = 2x - 3m\) (với \(m\) là tham số) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},{x_2}\) thỏa mãn điều kiện \({x_1}x_2^2 - {x_2}\left( {3m + 2{x_1}} \right) = 12\).
Bài 4. Trong giai đoạn phòng chống đại dịch Covid-19, Bộ Y tế khuyến cáo người dân thực hiện nghiêm túc thông điệp 5K, trong đó có yêu cầu giữ vệ sinh và “Khử khuẩn”.
Theo kế hoạch một công ty phải sản xuất \(4000\) chai dung dịch khử khuẩn trong một thời gian quy định (số chai dung dịch khử khuẩn sản xuất trong mỗi ngày là bằng nhau). Để tăng cường phòng chống dịch, mỗi ngày công ty đã sản xuất nhiều hơn dự định \(100\) chai dung dịch khử khuẩn. Do đó, công ty đã hoàn thành công việc trước thời hạn \(2\) ngày. Hỏi theo kế hoạch, mỗi ngày công ty sản xuất bao nhiêu chai dung dịch khử khuẩn?
Bài 5. Từ điểm \(S\) nằm ngoài đường tròn tâm \(O\), vẽ hai tiếp tuyến \(SA,SB\) với đường tròn (\(A,B\) là các tiếp điểm) và cát tuyến \(SCD\) không đi qua \(O(C\) nằm giữa \(S\) và \(D)\). Gọi \(K\) là giao điểm của \(SO\) với cung nhỏ \(AB\) và \(H\) là giao điểm của \(SO\) với đoạn thẳng \(AB\). Chứng minh:
a) Tứ giác \(SAOB\) nội tiếp;
b) \(S{A^2} = SC.SD\);
c) \(\angle SCK = \angle HCK\).
Bài 6. Công trình vòng xoay đường Trần Hưng Đạo và đường Lê Hồng Phong ở Thành phố Sóc Trăng có mô hình của một quả địa cầu với đường kính bằng \(5\) mét, bề mặt được làm từ tấm hợp kim. Tính diện tích mặt cầu ứng với mô hình đó.
Lời giải
Bài 1
Phương pháp:
Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)
Thực hiện các phép tính với căn bậc hai.
Cách giải:
\(\begin{array}{l}A = 3\sqrt {48} + \sqrt {75} - 2\sqrt {108} \\\,\,\,\,\, = 3\sqrt {16.3} + \sqrt {25.3} - 2\sqrt {36.3} \\\,\,\,\,\, = 12\sqrt 3 + 5\sqrt 3 - 12\sqrt 3 \\\,\,\,\,\, = \left( {12 + 5 - 12} \right)\sqrt 3 \\\,\,\,\,\, = 5\sqrt 3 \end{array}\)
Vậy \(A = 5\sqrt 3 \).
Bài 2
Phương pháp:
a) Sử dụng phương pháp cộng đại số, tìm được nghiệm \(y\)
Sử dụng phương pháp thế, tìm được nghiệm \(x\)
Kết luận nghiệm \(\left( {x;y} \right)\) của hệ phương trình.
b) Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\)
Phương trình ban đầu trở thành phương trình bậc hai một ẩn: \(a{t^2} + bt + c = 0\left( {a \ne 0} \right)\)
Tính \(\Delta \), sử dụng công thức nghiệm của phương trình bậc hai một ẩn, tìm được \(t\), lấy \(t\) thỏa mãn điều kiện
Với \(t\) tìm được, ta tìm được \(x\) tương ứng.
Cách giải:
a) \(\left\{ \begin{array}{l}2x + 3y = 8\\ - x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 3y = 8\\ - 2x + 2y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 10\\ - x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\)
Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {1;2} \right)\).
b) \({x^4} + 7{x^2} - 18 = 0\)
Đặt \(t = {x^2}\left( {t \ge 0} \right)\), phương trình ban đầu trở thành: \({t^2} + 7t - 18 = 0\)
Ta có: \(\Delta = {7^2} - 4.1.\left( { - 18} \right) = 121 = {11^2} > 0\) nên phương trình có 2 nghiệm phân biệt:
\(\left[ \begin{array}{l}{t_1} = \dfrac{{ - 7 + 11}}{2} = 2\left( {tm} \right)\\{t_2} = \dfrac{{ - 7 - 11}}{2} = - 9\left( {ktm} \right)\end{array} \right.\)
Với \(t = 2\) ta có: \({x^2} = 2 \Leftrightarrow x = \pm \sqrt 2 \).
Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm \sqrt 2 } \right\}\).
Bài 3
Phương pháp:
a) Vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
+ Nhận xét về hệ số \(a\) và sự biến thiên của hàm số
+ Lập bảng giá trị tương ứng của \(x\) và \(y\)
+ Xác định được các điểm mà đồ thị đi qua, vẽ đồ thị.
b) + Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) (Phương trình \(\left( * \right)\))
+ \(\left( d \right)\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},{x_2}\) \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \({x_1},{x_2} \Leftrightarrow \Delta ' > 0\)
+ Áp dụng hệ thức Vi – ét, tính được \({x_1}{x_2};{x_1} + {x_2}\), thay vào phương trình của đề bài và giải.
Cách giải:
a) Vì \(a > 1\) nên parabol (P): \(y = {x^2}\) có bề lõm hướng lên và nhận \(Oy\) làm trục đối xứng.
Hàm số đồng biến khi \(x > 0\) và nghịch biến khi \(x < 0\).
Ta có bảng giá trị tương ứng của \(x\) và \(y\):
|
\(x\) |
\( - 2\) |
\( - 1\) |
\(0\) |
\(1\) |
\(2\) |
|
\(y = {x^2}\) |
\(4\) |
\(1\) |
\(0\) |
\(1\) |
\(4\) |
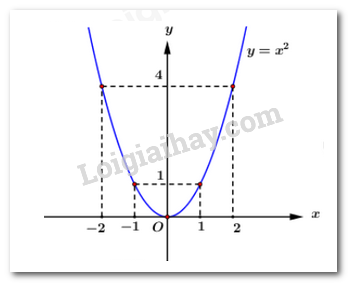
Suy ra parabol \(\left( P \right):y = {x^2}\) đi qua các điểm \(\left( { - 2;4} \right),\left( { - 1;1} \right),\left( {0;0} \right),\left( {1;1} \right),\left( {2;4} \right)\).
Ta có đồ thị parabol \(\left( P \right):y = {x^2}\):
b) Xét phương trình hoành độ giao điểm:
\(\begin{array}{l}\,\,\,\,\,\,\,\,{x^2} = 2x - 3m\\ \Leftrightarrow {x^2} - 2x + 3m = 0\,\,\,\left( * \right)\end{array}\)
Để đường thẳng \(\left( d \right):y = 2x - 3m\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1};{x_2}\) thì phương trình (*) phải có hai nghiệm \({x_1};{x_2}.\)
\(\begin{array}{l} \Leftrightarrow \Delta ' > 0\\ \Leftrightarrow 1 - 3m > 0\\ \Leftrightarrow m < \dfrac{1}{3}\end{array}\)
Theo định lí Viet, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = 3m\end{array} \right.\)
Vì \({x_2}\) là nghiệm của phương trình (*) nên \(x_2^2 - 2{x_2} + 3m = 0 \Leftrightarrow 3m = 2{x_2} - x_2^2\)
\(\begin{array}{l} \Rightarrow {x_1}x_2^2 - {x_2}\left( {2{x_2} - x_2^2 + 2{x_1}} \right) = 12\\ \Leftrightarrow {x_1}x_2^2 + x_2^3 - 2{x_2}\left( {{x_1} + {x_2}} \right) = 12\\ \Leftrightarrow x_2^2\left( {{x_1} + {x_2}} \right) - 2{x_2}\left( {{x_1} + {x_2}} \right) = 12\\ \Leftrightarrow \left( {{x_1} + {x_2}} \right)\left( {x_2^2 - 2{x_2}} \right) = 12\\ \Leftrightarrow 2x_2^2 - 4{x_2} = 12\\ \Leftrightarrow x_2^2 - 2{x_2} = 6\\ \Rightarrow - 3m - 6 = 0\\ \Leftrightarrow m = - 2\left( {tm} \right)\end{array}\)
Vậy \(m = - 2\).
Bài 4
Phương pháp:
Gọi số chai dung dịch khử khuẩn mỗi ngày công ty đó sản xuất theo kế hoạch là \(x\) (chai, \(x \in \mathbb{N}*\)).
Tính được thời gian sản xuất theo kế hoạch
Tính được số chai sản xuất trong một ngày và thời gian sản xuất theo thực tế
Từ giả thiết thời gian hoàn thành của kế hoạch và thực tế, lập được phương trình, giải phương trình, đối chiếu điều kiện và kết luận.
Cách giải:
Gọi số chai dung dịch khử khuẩn mỗi ngày công ty đó sản xuất theo kế hoạch là \(x\) (chai, \(x \in \mathbb{N}*\)).
Thời gian để sản xuất \(4000\) chai dung dịch khử khuẩn theo kế hoạch là \(\dfrac{{4000}}{x}\) (ngày).
Thực tế mỗi ngày công ty đó sản xuất được \(x + 100\) (chai).
Thời gian thực tế để sản xuất \(4000\) chai dung dịch khử khuẩn là \(\dfrac{{4000}}{{x + 100}}\) (ngày).
Vì công ty đã hoàn thành công việc trước thời hạn \(2\) ngày nên ta có phương trình:
\(\dfrac{{4000}}{x} - \dfrac{{4000}}{{x + 100}} = 2\)
\(\begin{array}{l} \Rightarrow 4000\left( {x + 100} \right) - 4000x = 2x\left( {x + 100} \right)\\ \Leftrightarrow 2{x^2} + 200x - 400000 = 0\\ \Leftrightarrow {x^2} + 100x - 200000 = 0\end{array}\)
Ta có: \(\Delta ' = {50^2} + 200000 = 202500 = {450^2} > 0\) nên phương trình có hai nghiệm phân biệt:
\(\left[ \begin{array}{l}x = - 50 + 450 = 400(tm)\\x = - 50 - 450 = - 500\left( {ktm} \right)\end{array} \right.\)
Vậy số chai dung dịch khử khuẩn mỗi ngày công ty đó sản xuất theo kế hoạch là \(400\) chai.
Bài 5
Phương pháp:
a) Vận dụng dấu hiệu nhận biết tứ giác nội tiếp: Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.
b) Ta sẽ chứng minh: \(\Delta SAC \sim \Delta SDA\left( {g.g} \right) \Rightarrow S{A^2} = SC.SD\)
c) Chứng minh: \(\dfrac{{SC}}{{CH}} = \dfrac{{SO}}{{OA}}\); \(\dfrac{{SK}}{{KH}} = \dfrac{{SA}}{{AH}}\); \(\dfrac{{SO}}{{OA}} = \dfrac{{SA}}{{AH}}\)suy ra \(\dfrac{{SC}}{{CH}} = \dfrac{{SK}}{{KH}}\)
Do đó \(CK\) là tia phân giác của góc \(\angle SCH \Rightarrow \angle SCK = \angle HCK\).
Cách giải:
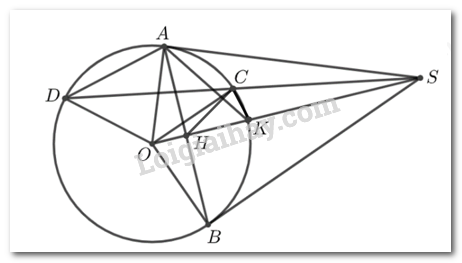
a) Ta có: \(\angle SAO = \angle SBO = {90^o}\) (vì \(SA,SB\) là tiếp tuyến của đường tròn \(\left( O \right)\)).
Xét tứ giác \(SAOB\) ta có: \(\angle SAO + \angle SBO = {90^o} + {90^o} = {180^o}\) nên tứ giác \(SAOB\) nội tiếp (dấu hiệu nhận biết)
b) Xét \(\Delta SAC\) và \(\Delta SDA\) ta có:
\(\angle ASD\) chung
\(\angle SAC = \angle SDA\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\)).
\( \Rightarrow \Delta SAC \sim \Delta SDA\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{SA}}{{SD}} = \dfrac{{SC}}{{SA}}\) (định nghĩa tam giác đồng dạng)
\( \Rightarrow S{A^2} = SC.SD\) (đpcm).
c) Áp dụng hệ thức lượng vào \(\Delta SAO\) vuông tại \(A\), đường cao \(AH\) ta có: \(SH.SO = SC.SD \Rightarrow \dfrac{{SH}}{{SD}} = \dfrac{{SC}}{{SO}}(*)\)
Xét \(\Delta SHC\) và \(\Delta SDO\) ta có:
\(\dfrac{{SH}}{{SD}} = \dfrac{{SC}}{{SO}}\)
\(\angle DSO\) chung
\( \Rightarrow \Delta SHC \sim \Delta SDO\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{SC}}{{HC}} = \dfrac{{SO}}{{DO}} = \dfrac{{SO}}{{OA}}\) hay \(\dfrac{{SC}}{{CH}} = \dfrac{{SO}}{{OA}}\) (1) (vì \(OD = OA = R\))
Xét \(\left( O \right):SA,SB\) là tiếp tuyến của đường tròn
\( \Rightarrow SA = SB\) (tính chất hai tiếp cắt nhau)
Lại có: \(OA = OB = R\)
\( \Rightarrow OS\) là đường trung trục của đoạn \(AB\)
Mà \(K \in OS \Rightarrow AK = BK\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow cungAK = cungBK\)
\( \Rightarrow \angle SAK = \angle KAB\) (cùng chắn 2 cung bằng nhau)
\( \Rightarrow AK\) là đường phân giác của \(\angle SAH\).
Theo tính chất đường phân giác của tam giác, ta có: \(\dfrac{{SK}}{{KH}} = \dfrac{{SA}}{{AH}}\) (2)
Xét \(\Delta SHA\) và \(\Delta SAO\) ta có:
\(\angle OSA\) chung
\(\angle SHA = \angle SAO = {90^o}\)
\( \Rightarrow \Delta SHA \sim \Delta SAO\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{SO}}{{OA}} = \dfrac{{SA}}{{AH}}\) (3)
Từ (1); (2) và (3) suy ra \(\dfrac{{SC}}{{CH}} = \dfrac{{SK}}{{KH}}\).
Do đó \(CK\) là tia phân giác của góc \(\angle SCH \Rightarrow \angle SCK = \angle HCK\).
Bài 6
Phương pháp:
Diện tích mặt cầu có bán kính \(R\) được tính theo công thức \(4\pi {R^2}\)
Cách giải:
Mặt cầu ứng với mô hình đó có bán kính \(R = 2,5m\) nên diện tích mặt cầu ứng với mô hình đó là:
\(S = 4\pi {R^2} = 4\pi .2,{5^2} = 25\pi \,\left( {{m^2}} \right)\)
Vậy diện tích mặt cầu ứng với mô hình đó là \(25\pi \,\left( {{m^2}} \right)\).












