Đề thi vào 10 môn Toán Bạc Liêu năm 2019
Tải vềCâu 1 (2 điểm): Rút gọn biểu thức
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Câu 1 (2 điểm): Rút gọn biểu thức
\(a)\,A = \sqrt {45} - 2\sqrt {20} \) \(b)\,B = \dfrac{{3\sqrt 5 - \sqrt {27} }}{{\sqrt 3 - \sqrt 5 }} - \sqrt {{{\left( {3 - \sqrt {12} } \right)}^2}} \)
Câu 2 (2,0 điểm):
a) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 4\\x + 4 = 5\end{array} \right.\)
b) Cho hàm số \(y = 3{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(\left( d \right):y = 2x + 1\) . Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Câu 3 (3,0 điểm)
Cho phương trình \({x^2} - 2mx - 4m - 5 = 0\,\,\left( 1 \right)\) (\(m\) là tham số)
a) Giải phương trình khi \(m = - 2\).
b) Chứng minh phương trình (1) luôn có hai nghiệm với mọi giá trị của \(m\).
c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình (1). Tìm \(m\) để: \(\dfrac{1}{2}x_1^2 - \left( {m - 1} \right){x_1} + {x_2} - 2m + \dfrac{{33}}{2} = 762019\).
Câu 4 (3,0 điểm) Trên nửa đường tròn, đường kính \(AB\), lấy hai điểm \(I,\,\,Q\) sao cho \(I\) thuộc cung \(AQ\). Gọi \(C\) là giao điểm hai tia \(AI\) và \(BQ\); \(H\) là giao điểm hai dây \(AQ\) và \(BI\).
a) Chứng minh tứ giác \(CIHQ\) nội tiếp.
b) Chứng minh \(CI.AI = HI.BI\).
c) Biết \(AB = 2R\). Tính giá trị của biểu thức \(M = AI.AC + BQ.BC\) theo \(R\).
Lời giải
Câu 1:
Phương pháp:
Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,\,A < 0\end{array} \right..\)
Cách giải:
\(a)\,A = \sqrt {45} - 2\sqrt {20} = \sqrt {{3^2}.5} - 2\sqrt {{2^2}.5} = \,3\sqrt 5 - 2.2\sqrt 5 = 3\sqrt 5 - 4\sqrt 5 = \, - \sqrt 5 \)
\(\begin{array}{l}b)\,B = \dfrac{{3\sqrt 5 - \sqrt {27} }}{{\sqrt 3 - \sqrt 5 }} - \sqrt {{{\left( {3 - \sqrt {12} } \right)}^2}} = \dfrac{{3\sqrt 5 - 3\sqrt 3 }}{{\sqrt 3 - \sqrt 5 }} - \left| {3 - \sqrt {12} } \right|\\\,\,\,\,\,\,\,\, = \dfrac{{3\left( {\sqrt 5 - \sqrt 3 } \right)}}{{\sqrt 3 - \sqrt 5 }} - \left( { - 3 + \sqrt {12} } \right)\,\,\left( {do\,\,{3^2} < 12\,\, \Rightarrow 3 < \sqrt {12} } \right)\\\,\,\,\,\,\,\,\, = - 3 + 3 - \sqrt {12} \, = - \sqrt {12} \, = - 2\sqrt 3 \end{array}\)
Câu 2 (VD):
Phương pháp:
a) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.
b) Số giao điểm của \(\left( P \right)\) và \(\left( d \right)\) chính bằng số nghiệm của phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\). Từ đó ta tìm được giao điểm của \(\left( P \right)\) và \(\left( d \right)\).
Cách giải:
a) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 4\\x + y = 5\end{array} \right.\)
\(\left\{ \begin{array}{l}2x - y = 4\\x + y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 9\\y = 5 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\end{array} \right.\)
Vậy hệ phương trình có nghiệm là: \(\left( {x;y} \right) = \left( {3;2} \right)\)
b) Cho hàm số \(y = 3{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(\left( d \right):y = 2x + 1\) . Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.
Xét phương trình hoành độ giao điểm: \(3{x^2} = 2x + 1 \Leftrightarrow 3{x^2} - 2x - 1 = 0\,\,\left( * \right)\)
Phương trình \(\left( * \right)\) có hệ số: \(a = 3;\,\,\,b = - 2;\,\,\,c = - 1 \Rightarrow a + b + c = 3 - 2 - 1 = 0\).
\( \Rightarrow \left( * \right)\) có hai nghiệm \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \dfrac{c}{a} = \dfrac{{ - 1}}{3}\end{array} \right.\)
Với \(x = 1 \Rightarrow y = 3{x^2} = {3.1^2} = 3\,\, \Rightarrow A\left( {1;3} \right)\)
Với \(x = \dfrac{{ - 1}}{3} \Rightarrow y = 3{x^2} = 3.{\left( {\dfrac{{ - 1}}{3}} \right)^2} = \dfrac{1}{3} \Rightarrow B\left( {\dfrac{{ - 1}}{3};\,\dfrac{1}{3}} \right)\)
Vậy tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\)là \(A\left( {1;3} \right)\) và \(\left( {\dfrac{{ - 1}}{3};\dfrac{1}{3}} \right)\)
Câu 3 (VD):
Phương pháp:
a) Thay \(m = - 2\) vào phương trình và giải phương trình bậc hai.
b) Chứng minh \(\Delta > 0\,\,\forall m\), sử dụng hằng đẳng thức.
c) Áp dụng định lí Vi-ét.
Cách giải:
a) Thay \(m = - 2\) vào phương trình (1) ta có: \({x^2} + 4x + 3 = 0\).
\(\begin{array}{l} \Leftrightarrow {x^2} + 3x + x + 3 = 0 \Leftrightarrow x\left( {x + 3} \right) + \left( {x + 3} \right) = 0\\ \Leftrightarrow \left( {x + 3} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\end{array} \right.\end{array}\)
Vậy khi \(m = - 2\) thì phương trình có tập nghiệm \(S = \left\{ { - 3; - 1} \right\}\).
b) Ta có \(\Delta ' = {m^2} - \left( { - 4m - 5} \right) = {m^2} + 4m + 5 = {\left( {m + 2} \right)^2} + 1 > 0\,\,\forall m\).
Do đó phương trình (1) luôn có hai nghiệm với mọi giá trị của \(m\).
c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình (1). Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = - 4m - 5\end{array} \right.\)
Theo bài ra ta có: \(\dfrac{1}{2}x_1^2 - \left( {m - 1} \right){x_1} + {x_2} - 2m + \dfrac{{33}}{2} = 762019\)
\(\begin{array}{l} \Leftrightarrow x_1^2 - 2\left( {m - 1} \right){x_1} + 2{x_2} - 4m + 33 = 1524038\\ \Leftrightarrow x_1^2 - 2m{x_1} - 4m - 5 + 2\left( {{x_1} + {x_2}} \right) = 1524000\end{array}\)
Do \({x_1}\) là nghiệm của phương trình \(\left( 1 \right) \Rightarrow x_1^2 - 2m{x_1} - 4m - 5 = 0\).
\( \Rightarrow 2\left( {{x_1} + {x_2}} \right) = 1524000 \Leftrightarrow 2.2m = 1524000 \Leftrightarrow m = 381000\).
Vậy \(m = 381000\) thỏa mãn yêu cầu bài toán.
Câu 4 (VD):
Cách giải:
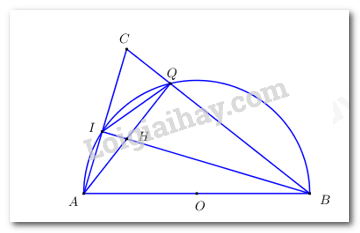
a) Chứng minh tứ giác \(CIHQ\) nội tiếp.
Ta có \(\angle AIB = \angle AQB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle CIH = \angle CQH = {90^0}\).
Xét tứ giác \(CIHQ\) có: \(\angle CIH + \angle CQH = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(CIHQ\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh \(CI.AI = HI.BI\).
Xét tam giác \(AHI\) và tam giác \(BCI\) có:
\(\angle AIH = \angle BIH = {90^0};\)
\(\angle IAH = \angle IBC\) (hai góc nội tiếp cùng chắn cung \(IQ\));
c) Biết \(AB = 2R\). Tính giá trị của biểu thức \(M = AI.AC + BQ.BC\) theo \(R\).
Ta có:
\(\begin{array}{l}M = AI.AC + BQ.BC\\\,\,\,\,\,\,\, = AC\left( {AC - IC} \right) + BQ\left( {BQ + QC} \right)\\\,\,\,\,\,\,\, = A{C^2} - AC.IC + B{Q^2} + BQ.QC\\\,\,\,\,\,\,\, = A{Q^2} + Q{C^2} - AC.IC + B{Q^2} + BQ.QC\\\,\,\,\,\,\,\, = \left( {A{Q^2} + B{Q^2}} \right) + QC\left( {QC + BQ} \right) - AC.IC\\\,\,\,\,\,\,\, = A{B^2} + QC.BC - AC.IC\end{array}\)
Tứ giác \(AIQB\) là tứ giác nội tiếp đường tròn \(\left( O \right) \Rightarrow \angle CIQ = \angle CBA\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Xét tam giác \(CIQ\) và tam giác \(CBA\) có:
\(\angle ACB\) chung;
\(\angle CIQ = \angle CBA\,\,\left( {cmt} \right);\)
Vậy \(M = AI.AC + BQ.BC = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\).












